Manacher

Manacher

Manacher 俗称“马拉车”，可以以 $O(n)$ 的代价求出以每一个位置为回文中心时的回文半径。

比较常见的暴力算法，即枚举以每一个点为回文中心向外拓展，直至不满足回文条件，时间复杂度为 $O(n^2)$。

那 Manacher 又是通过什么样的方式将复杂度降到了线性阶呢？

1. 预处理数组

众所周知，回文串可以看成是一个对称的字符串，即正着念倒着念都一样，但这就会引发一个问题，回文串长度为奇数和偶数时，其回文中心可能会落在某个字符上（奇数时），也可能落在两个字符中间（偶数时），诚然分类讨论可以解决，但代码量就是两倍，比较冗长。

这时便出现了预处理数组，具体的预处理手段说来也很简单，以一个==不会出现在字符串的字符==来分隔原字符串。

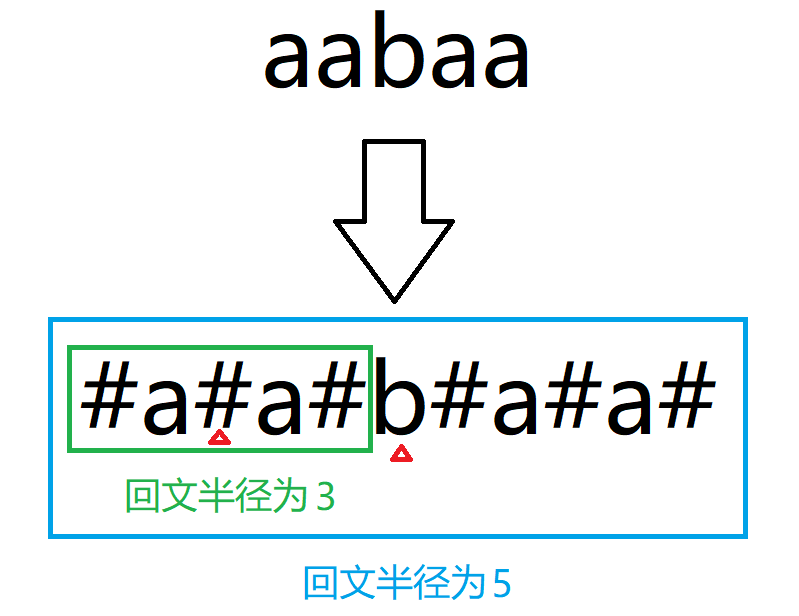
这样就不会出现回文半径在两个字符之间的情况了，能够很好地将奇偶情况结合起来，最后将预处理数组求出来的 回文半径/2 就是原来字符串的回文半径。

// 在预处理字符串的头和尾插入不同的字符可以不用额外判断越界
// 当然插入头尾的这两个字符也不能是字符串中出现过的
StringBuilder sb = new StringBuilder("$#");
for (int i = 0; i < len; i++) {
    sb.append(s.charAt(i) + "#");
}
len = sb.length();
sb.append("?");

2. 求回文半径

在求回文半径之前，要引入两个新的变量，一个是 right （拓展到过的最右下标），一个是 center （最右下标对应的回文中心）。

对于任何一个字符（下标为 i），必然满足以下两种情况。

• i > right，没有办法优化，只能暴力拓展。

• i <= right，设 i’ 为该点关于 center 对称的点，radius 为其最大回文半径。

  • 以 i’ 为回文中心的回文串在 right 内，即 i + radius < right。

    

    显然，此时 i 的最大回文半径等于 i’ 的最大回文半径，即 radius。

  • 以 i’ 为回文中心的回文串在 right 外，即 i + radius > right。

    

    此时，i 的最小回文半径为 right - i，至于多大，需要向外暴力拓展。

  • 以 i’ 为回文中心的回文串在 right 上 ，即 i + radius = right。

    

    此时，i 的最小回文半径为 radius，至于多大，需要向外暴力拓展。

对于上述四种情况，我们可以统一一种写法。

// i > right，最小回文半径为1，即它自己
// i <= right:
// 如果以i'为回文中心的回文串在right内，radius[center - (i - center)] 会是最小的
// 如果以i'为回文中心的回文串在right外，right - i 会是最小的
// 如果以i'为回文中心的回文串在right上，两者相同
radius[i] = i <= right ? Math.min(radius[center - (i - center)], right - i) : 1;

对四种情况都进行暴力拓展，虽然情况 2.1 不需要向外拓展，但即使拓展了也只会拓展一次，失败就退出了，而好处却可以缩短代码。

int[] radius = new int[len];
int center = -1, right = -1;
for (int i = 1; i < len; i++) {
    radius[i] = i <= right ? Math.min(radius[center - (i - center)], right - i) : 1;
    // 如果未在首尾添加额外字符，这里需要判断越界
    while (sb.charAt(i + radius[i]) == sb.charAt(i - radius[i])){
        radius[i]++;
    }
    // 如果新拓展的位置超过了原来的右边界，更新
    if (i + radius[i] - 1 > right){
        right = i + radius[i] - 1;
        center = i;
    }
}