单调栈

单调栈，顾名思义，在栈中维持了一个单调性，再配合其特有的先进后出的性质，可以很容易求出在某个数的左边和右边离它最近的大于（或小于）它的数。

这里使用递增的栈作为例子，递减同理。

有数组 **arr = [3, 5, 6, 2, 9, 4, 1]**，现在要求出距离每个点左边和右边最近的小于它的数的下标。

开始时，栈空。

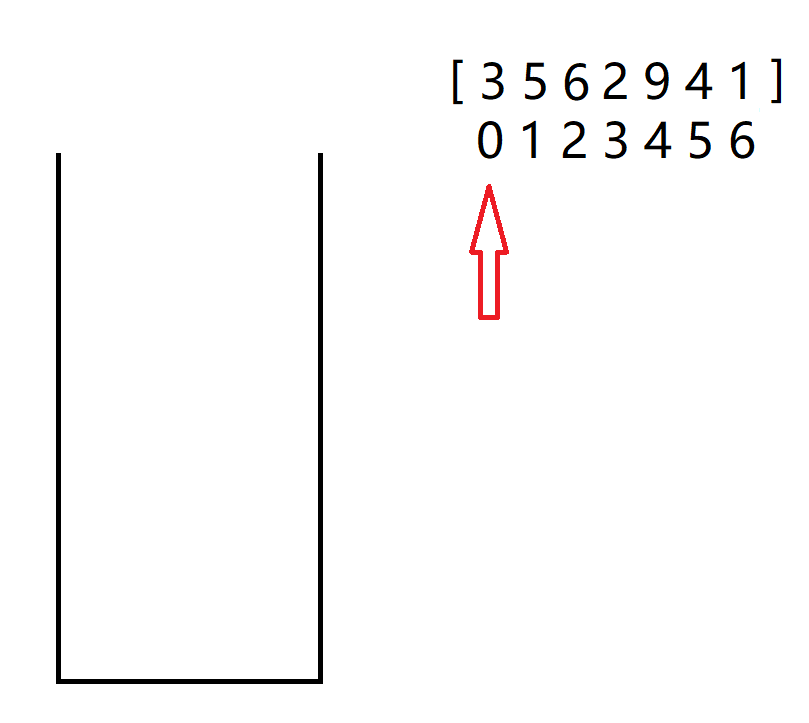
秉承着递增的规则，只要当前数大于栈顶元素，直接入栈。

==PS：说是这么说，但实际上都是放入该数的下标，因为下标所蕴含的信息可比单单一个数多，下标只需要通过原数组就能转换为其中的元素了。==

当遍历到 2 的时候，栈顶元素为 6（arr[2]） ，此时若将 2 入栈则不满足单调递增，也就是说，这个 2 是栈顶元素 6 的右边离他最近且比他小的数。

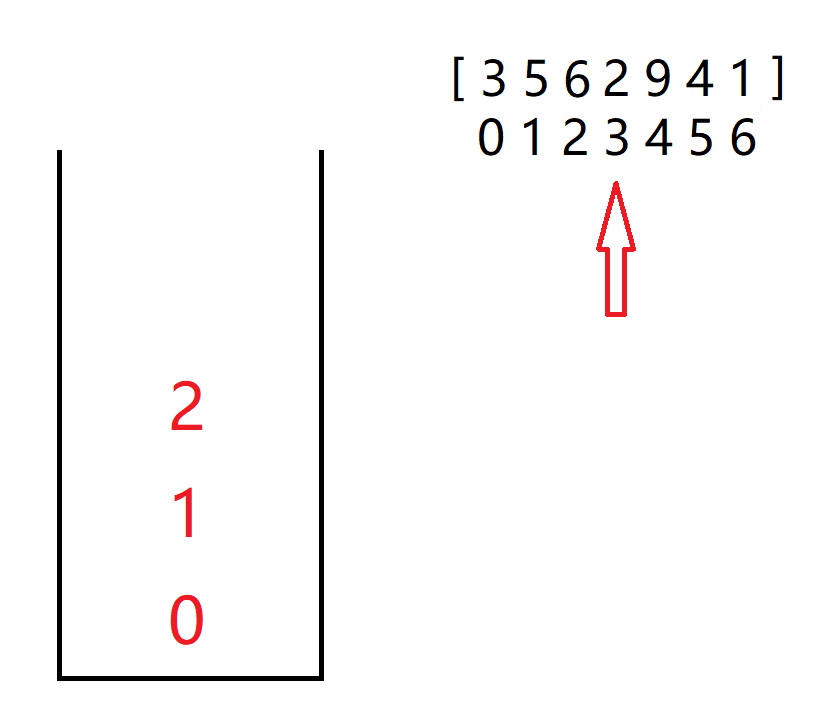
将栈顶元素弹出，并在 right 数组中记录 right[2] = 3，因为我们是依据递增性入栈，栈顶元素最大，在其被弹出后，新的栈顶成为了最大的元素，也就是老栈顶左边的离它最近且小于它的元素，记 left[2] = 1。

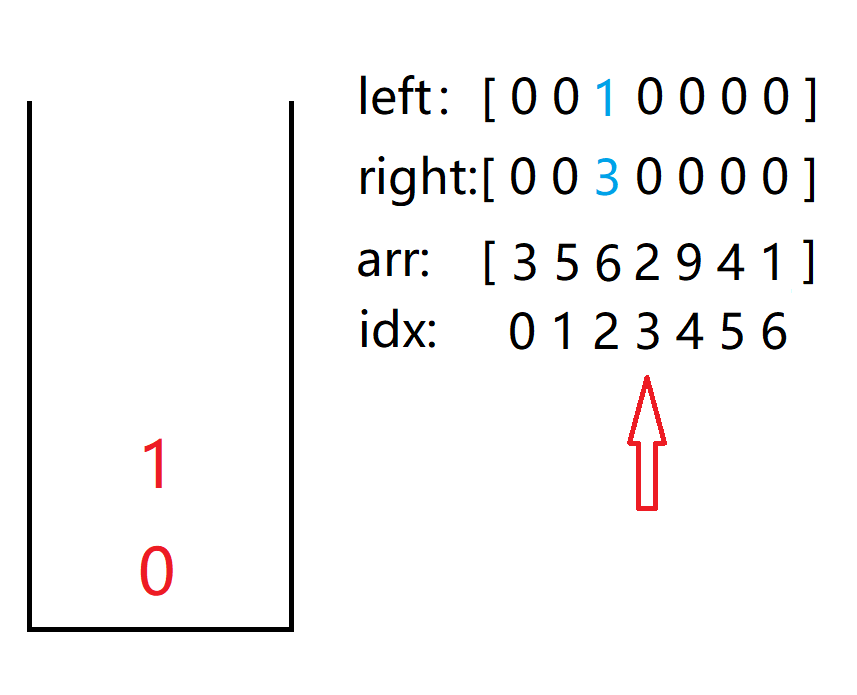
之后新上位的 5 接着和 2 作比较，循环往复，直至可以将 2 入栈且能维持递增性。

==注意：当栈顶元素弹出后，栈空，说明左边没有比其更小的数了，用 -1 表示。==

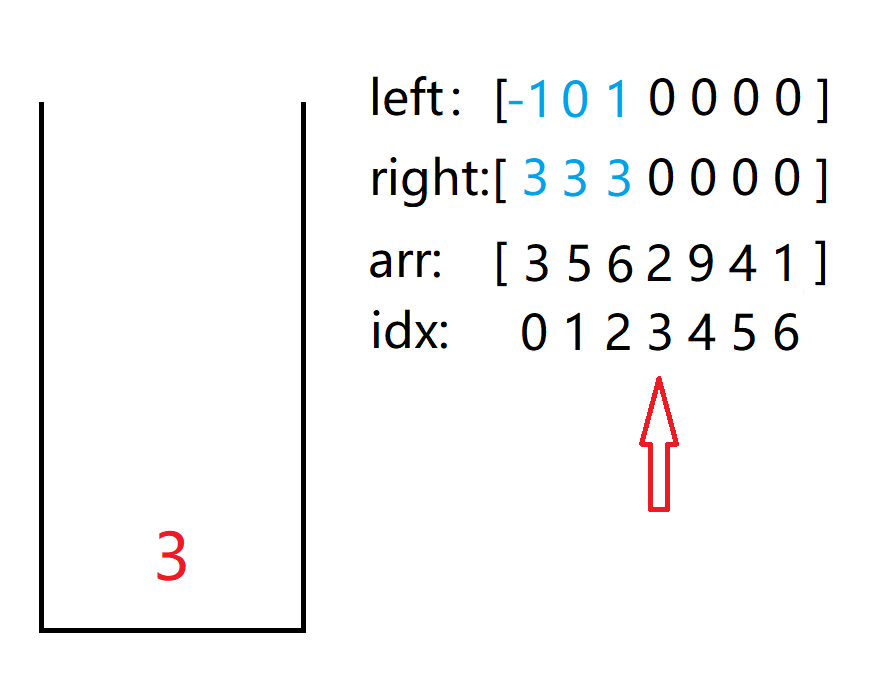
**right[i] **很好理解，毕竟只要遇见降序就会被记录下来，可 left[i] 要怎么理解呢？怎么能保证次栈顶是栈顶左侧离它最近且小于它的数呢？

可以看一下下面的图，绿线处代表出现递减，在其左侧且高于绿线的点会被弹出，并记录答案，而低于绿线的点因为还没有发现右侧离它最近且小于它的点，按兵不动。

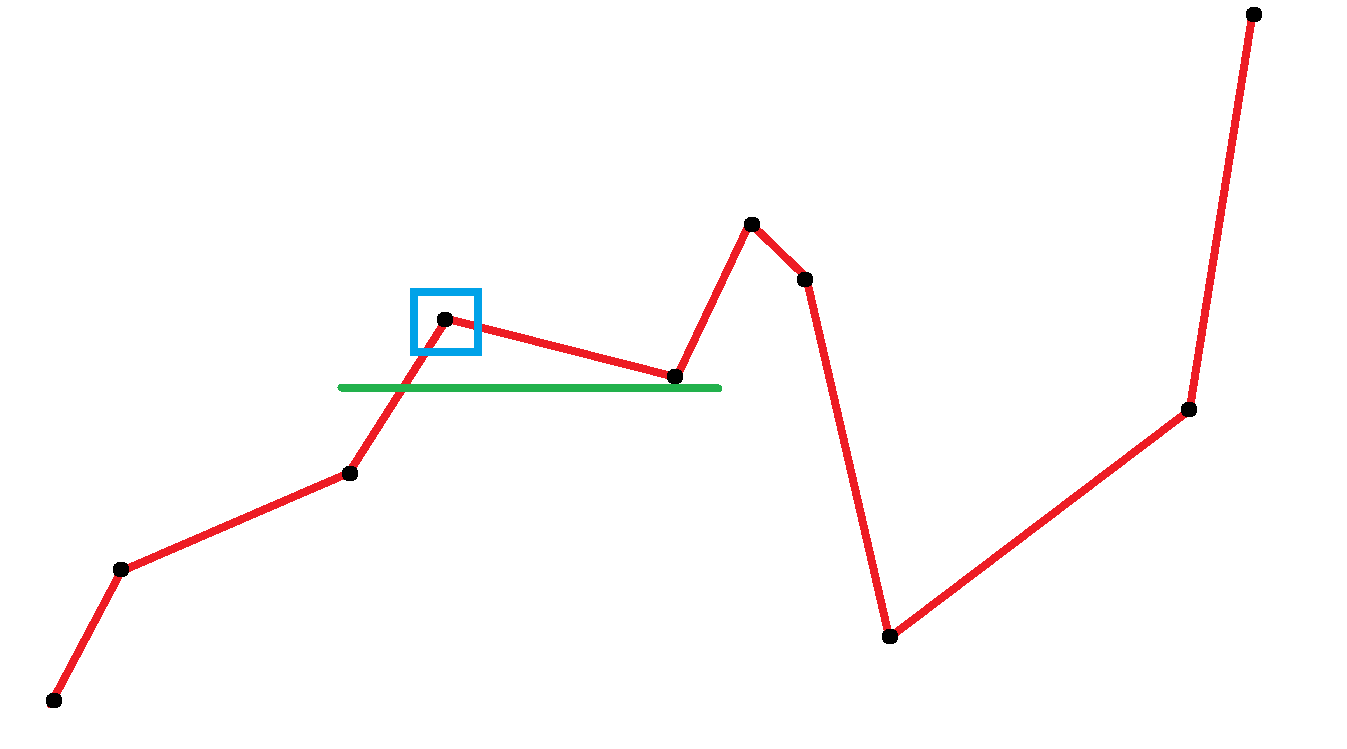
将该点从栈中弹出后并不会对后续答案产生纰漏，因为在该点以前的点都比该点小（该点以前的点不会拿该点当 right），且在该点后面位置出现了比该点更小的数（该点以后的点不会拿该点当 left），而该点也找到了其左右答案。

后续同理。

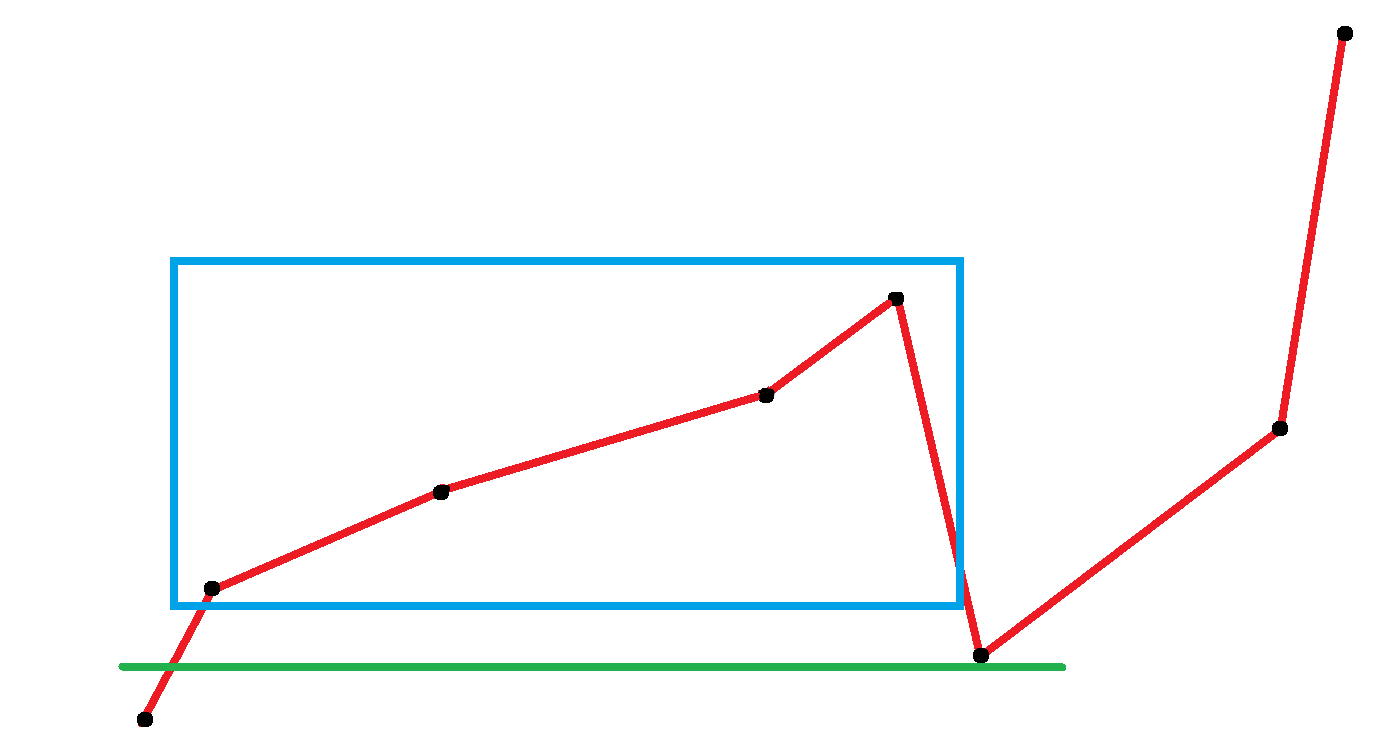
最后当数组遍历完成，而栈中还有元素时，说明此时栈中的元素右侧都没有比它小的数了，左侧比它小的数就是被其压在下面的数。

==同理，递减栈可用于求出距离每个元素最近且大于其的元素。==