KMP

一个人能走得多远并不取决于他顺境时能走的多块，而在于他逆境时能多快找回曾经的自己。——KMP

上面这句话还是蛮能概括KMP算法的精髓，不过貌似动态规划都能这么解释…

KMP

KMP 是由 Knuth、Morris 和 Pratt 所发明的字符串匹配算法，其核心就是当遇到字符不匹配时由于已经知道此前匹配过的字符，因此没有必要重头开始匹配！只要从某个已知字符起匹配即可。

具体做法就是先生成一个前后缀最长相等长度的数组，至于有什么用往下看就行了。

前后缀最长相等长度

这个一长串的名词是什么意思呢，举个例子，str = “123123”，那么它的前后缀最长相等长度就是 3（123 = 123），注意前后缀不能相等。

我们需要生成一个数组，这个数组存放着以 0 开头，以 i-1 结尾的子串的前后缀最长相等长度。

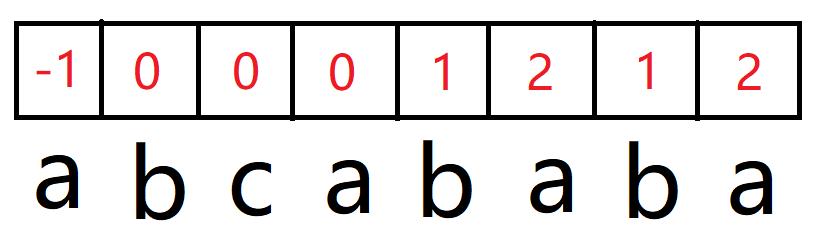
arr[0] 因为不存在在 0 之前的子串，因此没有意义，一律填 -1，而 arr[1] 也是固定填0（前后缀不能相等）。

后面需要经由状态转移变化而来，即该位前一位字符和之前的前后缀最长长度上的字符是否相等。

举个特殊的例子，abcabcb。c 前一位是 b，而 b 上的前后缀长度为 0，则需要判断 0 位置上的字符和 c 前一位的字符是否相等，a != c，所以填 0。

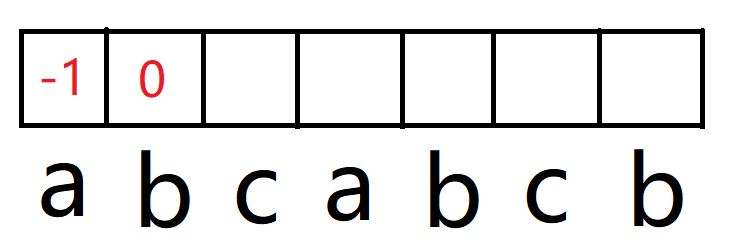
一直直到下标 5，也就是字符 b 所在位置，此时 b 的前一位 a 和该 a 所对前后缀长度为 0 的下标上的 a 相等，这里填 0 + 1 = 1。

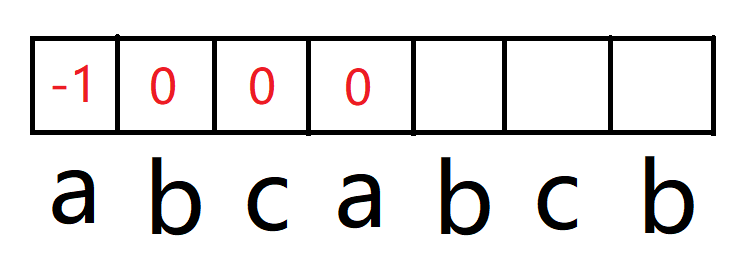
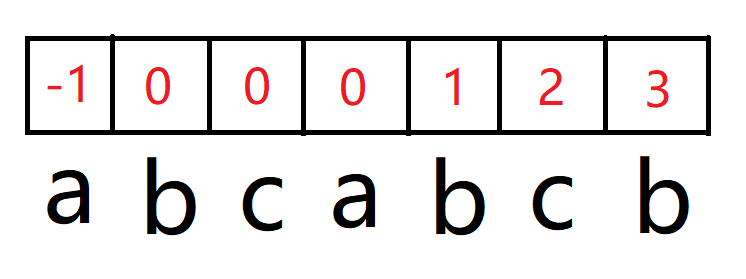
这里再详细讲一下最后一位是如何填的，下标为 6 的 b，前一位是下标为 5 的 a，而前后缀数组下标 5 上对应的是 2。

这个 2 则代表了蓝色区域等于绿色区域，因此我们只需要判断蓝色区域的下一个和绿色区域的下一个是否相同即可，这就是前后缀数组的强大之处了，这个2不仅代表了最长的前后缀，还代表了蓝色区域的下一位的下标，因为数组下标是从0开始计算的。

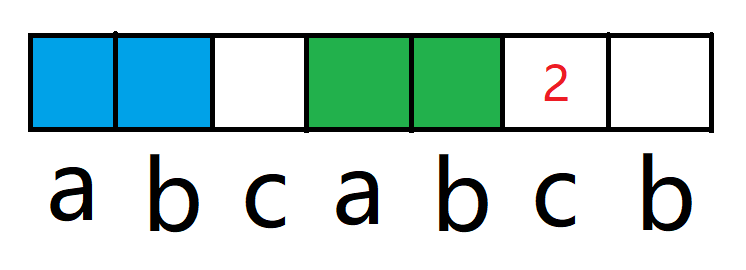
很自然地，我们判断了蓝色和绿色的下一位相等，那么该位上的前后缀长度就为上一位前后缀长度+1。

很明显，9 上的 b 不等于 4 上的 x。

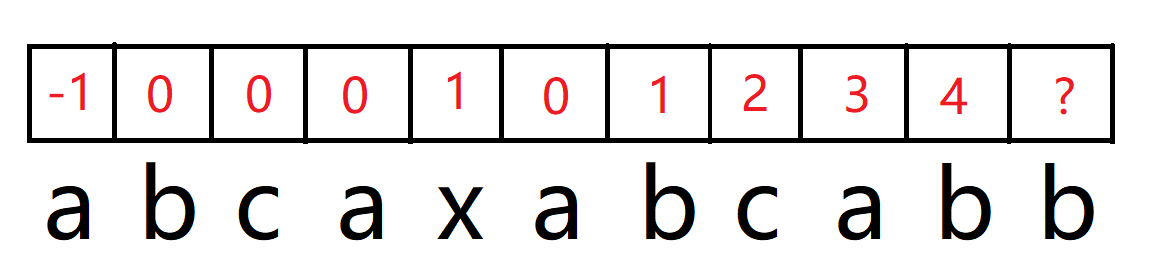
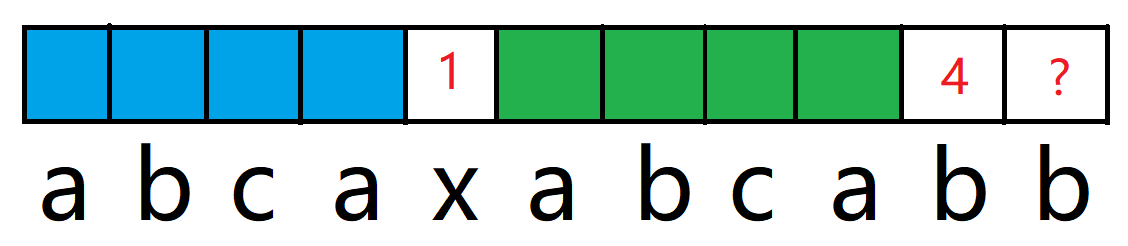
而下标 4 上的前后缀长度为 1，表明了下标 0 和 3 上字符相等，也就可以得到 0，3，5，8上的字符都相等，因此如果我们得到了下标 1 和下标 9 字符相等的话，不就仍然可以得到该位置之前的前后缀长度了吗，为前后缀数组下标为1的数值+1。

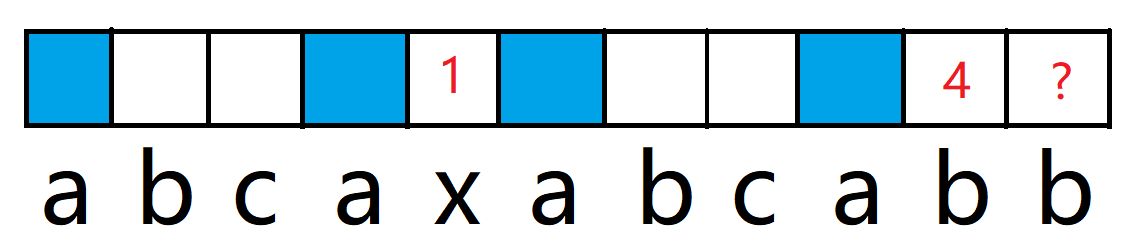
而如果我们一直迭代，到了0位置上的 -1也仍然没有发现匹配的字符，那么就填入-1 + 1 = 0，表示前后缀长度为 0。

public int[] getPrefix(char[] pattern) {
    int[] prefix = new int[pattern.length];
    prefix[0] = -1;
    for (int i = 2; i < pattern.length; i++) {
        int t = i - 1;
        while (t != 0 && pattern[i - 1] != pattern[prefix[t]]) {
            t = prefix[t];
        }
        prefix[i] = prefix[t] + 1;
    }
    return prefix;
}

==以上前后缀数组是求的 pattern 匹配子串的==

子串匹配

母串：abcabcabcb（指针i）

子串：abcabcb（指针j）

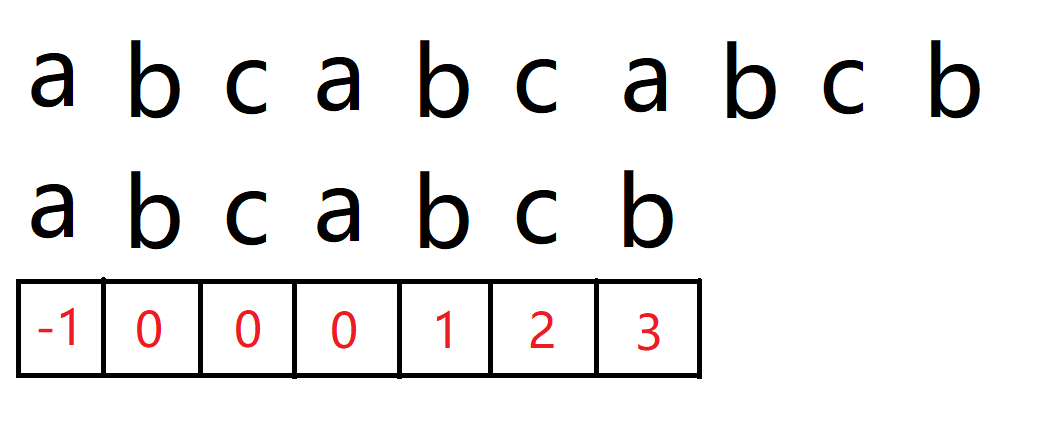
前面都没有问题，直到 i 和 j 指向下标 6，a != b，但由于我们是知道前面六个字符是 abcabc 的（==体现在该位置的前后缀长度为 3，具体是什么字符不重要==），没有必要再从头继续匹配。

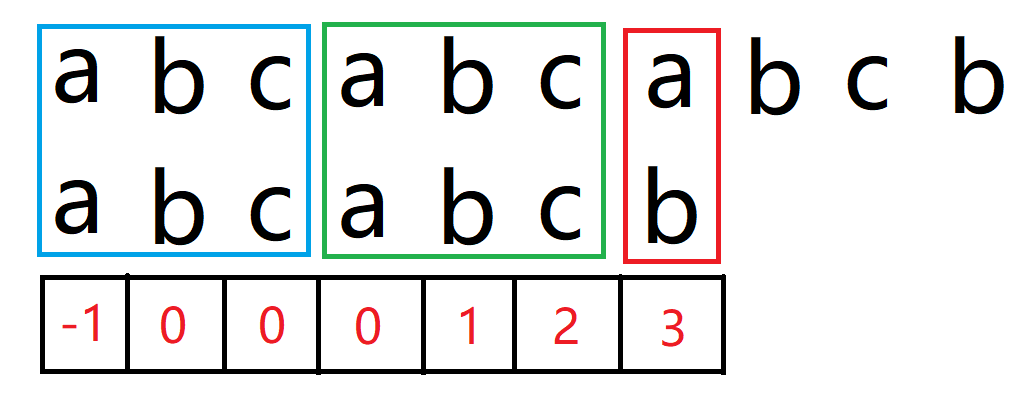
只需要将 j 退回到 3 即可，蓝色为已匹配，红色为待匹配。

若 j 指向0，仍然匹配不成功，i++。

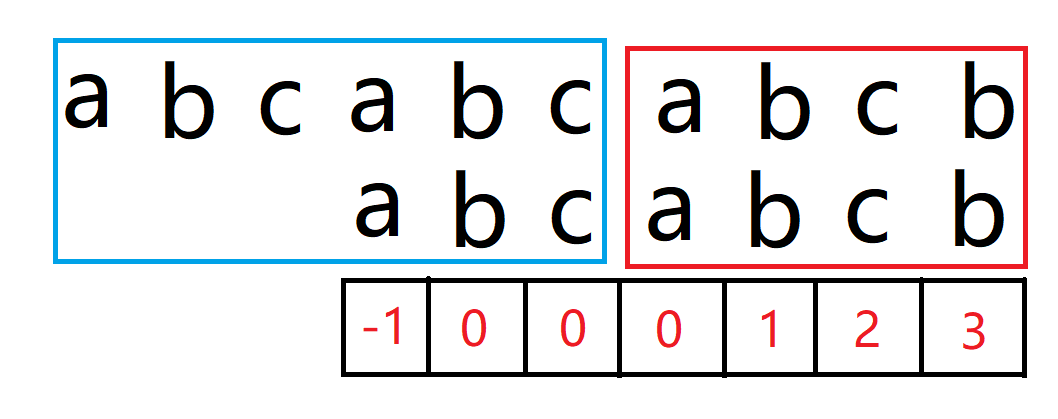
public int indexOf(String str1, String str2) {
    char[] chars1 = str1.toCharArray();
    char[] chars2 = str2.toCharArray();
    if (chars2.length == 0) {
        return 0;
    }
    int[] prefix = getPrefix(chars2);
    int l1 = 0;
    int l2 = 0;
    while (l1 < chars1.length && l2 < chars2.length) {
        if (chars1[l1] == chars2[l2]) {
            l1++;
            l2++;
        } else {
            if (l2 == 0) {
                l1++;
            } else {
                l2 = prefix[l2];
            }
        }
    }
    return l2 == chars2.length ? l1 - l2 : -1;
}

时间复杂度：O（n）

空间复杂度：O（n）