当我们在训练一个神经网络的时候,参数的随机初始化是非常重要的,对于逻辑回归来说,可以将权重初始化为0。而对于神经网络而言,这样做将会导致梯度下降算法无法起作用。
1. 为什么适用于逻辑回归?
如下图所示,其中$X_1$ 和 $X_2$ 是特征值。
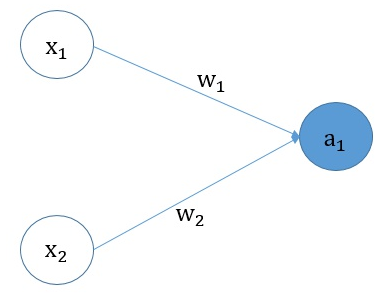
前向传播:
$a_1 = sigmoid(X_1 * W_1 + X_2 * W_2 + b)$
$loss = -ylog(a_1) - (1 - y)log(1 - a_1)$
反向传播:
$da_1 = -\frac{y}{a_1} + \frac{1 - y}{1 - a_1}$
$dw_1 = da_1 * a’_1 * X_1 = (a_1 - y) * X_1$
$dw_2 = da_1 * a’_1 * X_2 = (a_1 - y) * X_2$
$db = da_1 * a’_1 * 1 = a_1 - y$
参数更新:
$W_1 = w_1 - η * dw_1$
$W_2 = w_2 - η * dw_2$
$b = b - η * db$
可以看到, $W_1$ 和 $W_2$ 并不影响 $dw_1$ 和 $dw_2$ 的值,而是根据 $X_1$ 和 $X_2$ 的不同而改变,且不为0,模型的权重能够得到更新。因此即使我们将 $W_1$ 和 $W_2$ 初始化为0也无所谓。参数 同理。
2. 为什么不适用于神经网络?
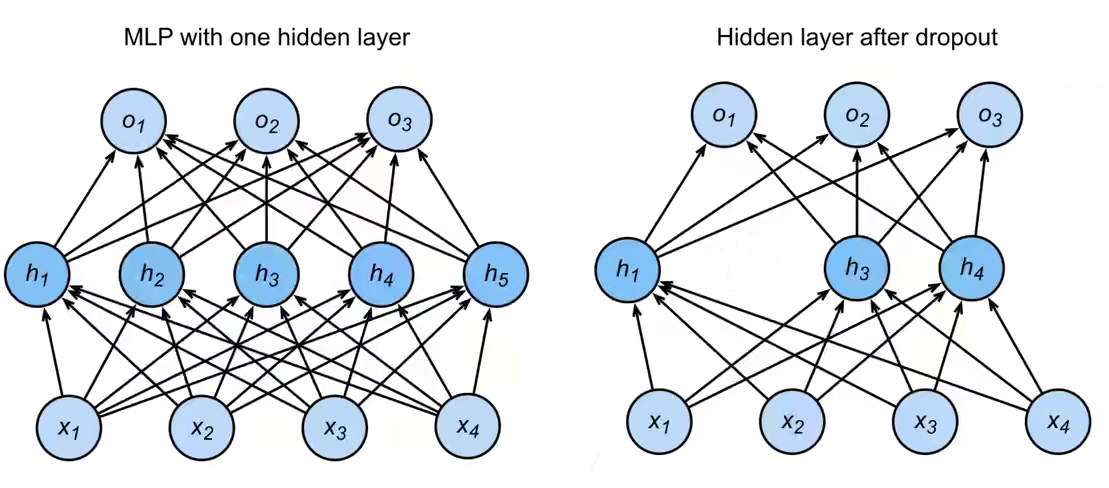
神经网络结构图如下。
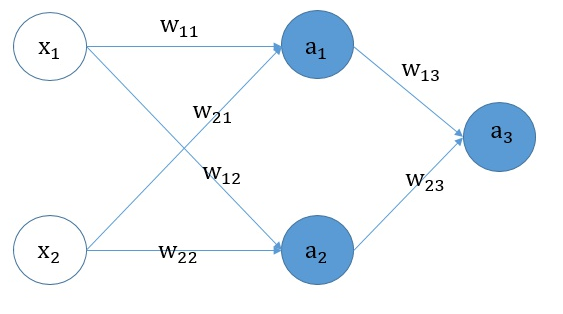
前向传播:
$a_1 = f(X_1 * W_{11} + X_2 * W_{21} + b_1)$
$a_2 = f(X_1 * W_{12} + X_2 * W_{22} + b_2)$
$a_3 = sigmoid(a_1 * W_{13} + a_2 * W_{23} + b_3)$
$loss = -ylog(a_3) - (1 - y)log(1 - a_3)$
反向传播:
$da_3 = -\frac{y}{a_3} + \frac{1 - y}{1 - a_3}$
$dw_{13} = da_3 * a’_3 * a_1 = (a_3 - y) * a_1$
$dw_{23} = da_3 * a’_3 * a_2 = (a_3 - y) * a_2$
$db_{3} = da_3 * a’_3 * 1 = a_3 - y$
$da_1 = da_3 * a’3 * W{13} = (a_3 - y) * W_{13}$
$da_2 = da_3 * a’3 * W{23} = (a_3 - y) * W_{23}$
$dw_{12} = da_2 * a’_2 * X_1$
$dw_{22} = da_2 * a’_2 * X_2$
$db_{2} = da_2 * a’_2$
$dw_{11} = da_1 * a’_1 * X_1$
$dw_{21} = da_1 * a’_1 * X_2$
$db_{1} = da_1 * a’_1$
参数更新:
$W_1 = w_1 - η * dw_1$
$W_2 = w_2 - η * dw_2$
$b = b - η * db$
根据上述的详细公式,我们分析一下3种情况:
- 模型所有权重 W 初始化为0,所有偏置 b 初始化为0
- 模型所有权重 W 初始化为0,所有偏置 b 随机初始化
- 模型所有的权重 W 随机初始化,所有偏置 b 初始化为0
2.1 模型所有权重 W 初始化为0,所有偏置 b 初始化为0
在此情况下, 第一个 batch 的前向传播过程时,$a_1 = f(0), a_2 = f(0), a_3 = sigmoid(0)$。在反向传播进行参数更新的时候,会发现 $a_1 = a_2 = f(0) \ \ =>\ \ dw_{13} = dw_{23}$,$W_{13} = W_{23} = 0 \ \ => \ \ da_1 = da_2 = 0$。也就是说,在第一个 batch 中,只有 $W_{13}$ 和 ${W_{23}}$ 进行了更新并且相等,而其它参数均没有更新。
而当第二个 batch 传给神经网络时,$W_{13} = W_{23} \neq 0 \ \ =>\ \ da_1 = da_2 \ \ => dw_{21} = dw_{22},\ dw_{11} = dw_{12}$。
以此类推,无论训练多少次,无论隐藏层神经元有多少个,由于权重的对称性,隐藏层神经单元的输出始终不变(权重相等)。我们希望不同的神经元能够有不同的输出,这样的神经网络才有意义。
总结:将权重 W 初始化为0,会导致同一隐藏层的所有神经元输出都一致。对于后期不同的 batch,每一隐藏层的权重都能得到更新,但是每一隐藏层神经元的权重都是一致的,多个隐藏神经元的作用就如同1个神经元。
2.2 模型所有权重 W 初始化为0,所有偏置 b 随机初始化
在此情况下,第一个 batch 的前向传播过程时,$a_1 = f(b_1), a_2 = f(b_2), a_3 = sigmoid(b_3)$,在反向传播过程时,$da_1 = da_2 = 0 \ \ => \ \ dw_{11} = dw_{12} = dw_{21} = dw_{22} = 0$,因此第一个 batch 中只有 $W_{13}, W_{23}$ 和 $B_{3}$ 能得到更新。
同理,在第二个 batch 反向传播的过程中,由于 $W_{13}$ 和 $W_{23}$ 不为0,因此所有的参数都能得到更新。这种方式存在更新较慢、梯度消失、梯度爆炸等问题,在实践中,通常不会选择该方法。
2.3 模型所有的权重 W 随机初始化,所有偏置 b 初始化为0
在此情况下,第一个 batch 的前向传播过程时,由于 $W_{13}$ 和 $W_{23}$ 不为0,因此所有的参数可以直接得到更新。
结论:在训练神经网络的时候,权重初始化要谨慎,不能初始化为0!