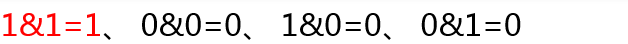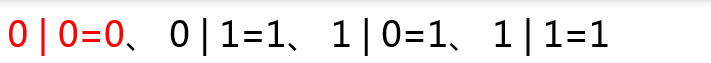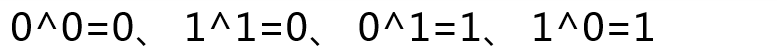位运算 位运算是程序设计中对位模式按位或二进制数的一元和二元操作。
一般情况下,位运算和加减运算的运算速度相当,且极大程度上快于乘除运算(10倍)。
很多编程语言都有位运算符,Java语言也不例外。在Java语言中,提供了7种位运算符,分别是 &(与)、|(或)、^(异或)、\~(非)、<<(左移)、>>(带符号右移)和>>>(无符号右移)。这些运算符当中,仅有 ~ 是单目运算符,其他运算符均为双目运算符。
位运算只能对 long 、int 、short 、byte 和 char 这五个整型类型数据进行运算,不能用于 double、float、boolean 以及其他 引用类型。
一、按位与运算 按位与运算符的写法是一个 & 符号,规则如下。
运算规则总结成一句话就是:如果两个二进制位上的数都是1,那么运算结果为1,其他情况运算结果均为0。下面举例说明按位与运算符的运算过程,我们用数字5和6进行按位与运算。这个过程可以用下图表示:
可以使用与运算来判断一个数是否是奇数。
1 2 3 4 public static void main (String[] args) System.out.println((788 & 1 ) == 1 ); System.out.println((789 & 1 ) == 1 ); }
二、按位或运算 按位或运算符的写法是一个 | 符号,规则如下。
运算规则概括成比较好记的一句话就是:两个二进制位上的数字如果都为0,那么运算结果为0,否则运算结果是1。同按位与运算一样,符号位也要参与运算。下面我们还是用5和6为例来讲解一下按位或的运算过程,如下图所示:
三、按位异或运算【重点】 按位或运算符的写法是一个 ^ 符号,规则如下。
如上图,运算规则为:两个二进制位上的数字如果相同,则运算结果为0,如果两个二进制位上的数字不相同,则运算结果为1。下面我们还是用5和6为例来讲解一下异或的运算过程,如下图:
异或运算的性质 $I$、异或运算满足交换律。
也就是说,a ^ b 与 b ^ a是等价的,虽然 a 和 b 交换了位置,但还是会运算出相同的结果。这个规律还可以推广到 N 个操作数,也就是说,如果有N个变量都参与了异或运算,那么它们的位置无论如何交换,运算的结果都是相同的。
$II$、任何两个相同的数字进行异或运算,所得到的结果为 0。
因为两个相同的数字,换算成补码后,每个二进制位上的数也都相同,这样在进行异或运算时,按照运算规则,每个二进制位上得到的运算结果也都是 0,这 N 个 0 所组成的二进制串就是数字 0 的补码。
可以判断两数是否相等:a ^ b = 0 -> a = b。
快速清零:a ^= a。
$III$、对于任意一个二进制位来说,这个位上的数与 0 进行异或运算,运算结果不变。
0 ^ 1 = 1,0 ^ 0 = 0,结果不变。
$IV$、对于任意一个二进制位来说,这个位上的数与 1 进行异或运算,运算结果取反。
1 ^ 0 = 1,1 ^ 1 = 0,结果取反。
$V$、对于任意两个整数 a 和 b,a ^ b ^ a = b 。
a ^ b ^ a = a ^ a ^ b = 0 ^ b = b。
这个特性在加密运算方面有着很普遍的应用。我们可以把 a 当作要加密的数据,而把 b 当作密钥。a 异或 b 就是把 a 用密钥 b 进行了加密操作,当需要解密时,仍然以 b 作为密钥,再进行一次异或就实现了解密。
四、按位取反运算 按位或运算符的写法是一个 ~ 符号,规则如下。
1 2 3 4 5 6 7 8 public class MyTest public static void main (String[] args) int a = 5 ; int b = ~a; System.out.println(a); System.out.println(b); } }
首先把数字5转换成补码形式,之后把每个二进制位上的数字进行取反,如果是0就变成1,如果1就变成0,经过取反后得到的二进制串就是运算结果,这个运算结果被还原为十进制数是-6。
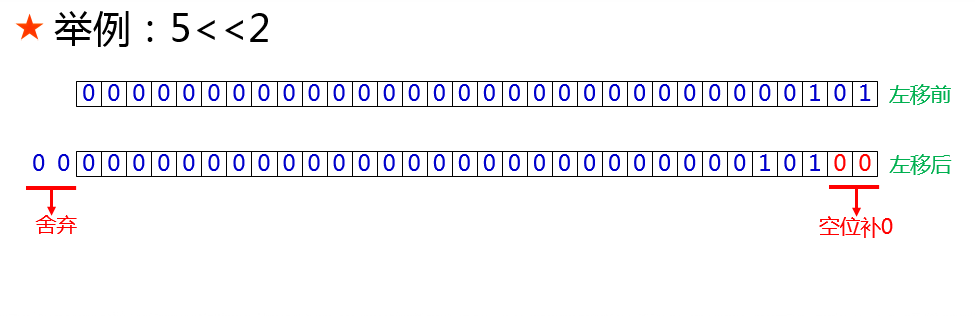
五、左移运算符 按位或运算符的写法是一个 << 符号,规则如下。
左移运算有乘以2的N次方的效果。一个数向左移动1位,就相当于乘以2的1次方,移动两位就相当于乘以2的2次方,也就是乘以4。位移操作在实际运算时远远快于乘法操作 ,所以在某些对运算速度要求非常高的场合,可以考虑用左移代替乘以2的N次方的乘法操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public static void main (String[] args) long start = System.currentTimeMillis(); for (int i=0 ;i<1e9 ;i++){ int a = i * 1024 ; } System.out.println(System.currentTimeMillis() - start); start = System.currentTimeMillis(); for (int i=0 ;i<1e9 ;i++){ int a = i << 10 ; } System.out.println(System.currentTimeMillis() - start); }
但当位移的位数很多时,导致最左边的符号位发生变化,就不再具有乘以2的N次方的效果了。比如十进制的5转换为补码形式是:前面29个0最后3位是101,如果移动29位,那么最前面的符号位就变成了1,此时运算的结果就成为了一个负数 ,不再是5乘以2的29次方的乘法结果。
1 2 3 4 5 6 public static void main (String[] args) int a = 5 ; System.out.println(a << 29 ); a = -5 ; System.out.println(a << 29 ); }
对于 byte/short/int 三种类型的数据,Java 语言最多支持31位的位移运算(包括下面的右移运算)。如果位移数超过31,则虚拟机会对位移数按连续减去32,直到得到一个小于32并且大于等于0的数 ,然后以这个数作为最终的位移数。
例如对 int 型变量进行位移97位的操作,虚拟机会首先对97连续减去3个32,最终得到数字1,实际进行位移运算时只对变量位移1位。
1 2 3 4 public static void main (String[] args) int a = 2 ; System.out.println(a << 97 ); }
而对于 long 类型的数据而言,最多支持63位的位移运算,如果位移数超过63,则连续减去64,以最终得到的小于64并且大于等于0的数作为位移数。小伙伴们可以试一下数字5左移32位是什么结果。
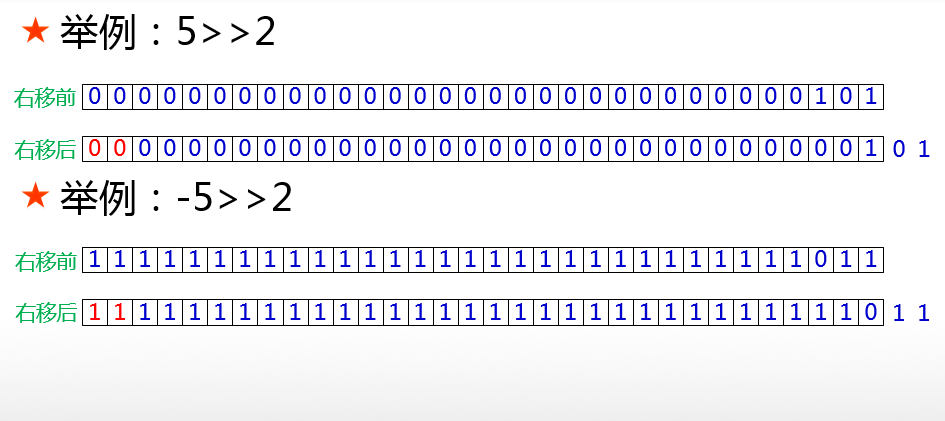
六、带符号右移运算符 右移运算分为两种,分别是带符号右移和无符号右移。首先我们来说说带符号右移运算符。带符号右移运算符的写法是 **>>**,与左移运算符的方向恰好相反。
带符号右移运算和左移运算类似,具有 /2 的功能,小数会被舍弃。
但是对于负数而言,带符号右移的效果分为两种情况,我们分别来讨论。
如果这个负数是“2的N次方”的整数倍,那么带符号右移N位的效果也等于除以2的N次方。举个例子:我们还是把N的值设为3,如果对于“-16”来说,它是“2的3次方”的整数倍,那么带符号右移3位的结果是-2,这个结果相当于“-16除以2的3次方”。
1 2 3 4 5 public static void main (String[] args) int a = -16 ; System.out.println(a >> 3 ); System.out.println(a / 8 ); }
而如果这个负数不是“2的N次方”的整数倍,那么右移N位之后,是在除以2的N次方的结果之上还要减去1。比如,对于-15来说,它不是“2的3次方”的整数倍,那么带符号右移3位的结果是-2,这个运算结果其实就是“-15被2的3次方整除再减去1”(减1是因为右移的时候丢弃了位数是 1 的位)。
1 2 3 4 5 public static void main (String[] args) int a = -15 ; System.out.println(a >> 3 ); System.out.println(a / 8 ); }
带符号右移的操作可以保证移动之前和移动之后数字的正负属性不变,原来是正数,不管移动多少位,移动之后还是正数,原来是负数,移动之后还是负数。
对于任何 一个byte、short 或者 int 类型的数据而言,带符号右移31位之后,得到的必然是 0 或者是 -1。对于 long 类型的数据而言,带符号右移 63 位之后,得到的也必然是 0 或者是 -1。
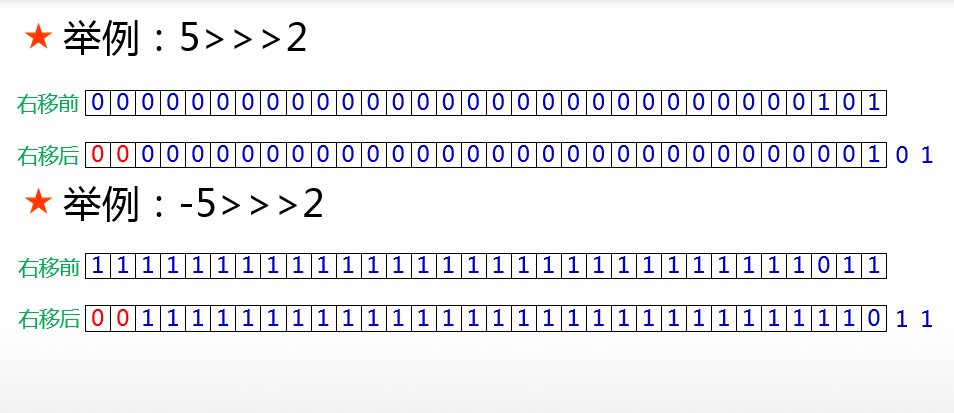
七、无符号右移运算符 无符号右移运算符的写法是 **>>>**,带符号右移的运算规则与无符号右移的运算规则差别就在于:无符号右移在二进制串移动之后,空位由0来补充,与符号位是0还是1毫无关系,如下图:
进行位运算的时候,最左边的符号位也是要参与运算的。