紫梦沁香
0%

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 61 阅读时长 ≈ 1 分钟

一、多模态大模型的发展历程

image-20240813130720971

二、多模态大模型的输入-输出空间

image-20240813130847622

（1）视觉编码器架构

image-20240813131006275

（2）离散化视觉表示

image-20240813131100131

（3）视觉编码器训练策略

image-20240813131216788

image-20240813131353454

发表于 更新于 阅读次数： Valine：
本文字数： 6.5k 阅读时长 ≈ 12 分钟

  1. 时间复杂度排序

    $n^n, n!, 9999n^{99}, n^{100}$​

  2. 输出a的值

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    int a = 0;

    int Fibo(int n){
        a++;
        if(n < 2) return 1;
        return Fibo(n-1) + Fibo(n-2);
    }

    int main(){
        Fibo(5);
        printf("%d", a);
    }

  3. 散列表

    散列表是数据结构的重点，经常会出现在选择和大题中，这里我额外出一道双散列的题目吧。
    表长为11，插入序列为45，72，54，28，99，83，66，67，散列函数为H(k)=k%11，再散列函数 Hi(k)= (H(k)+ i^2)%11，其中i为第i次冲突。插入完毕后，删除元素45。

    (1) 画出散列表
    (2) 查找成功的平均查找长度
    (3) 查找失败的平均查找长度
    (4) 装填因子

数据结构

第一章

1
时间复杂度是数据结构学习中的基础内容，虽然一般难度不高，但对同学们的细心和耐心要求较高。在学习和练习时，除了理解基本概念外，仔细审题是非常关键的一步。如果遇到难以理解的题目，建议同学不要急于求成，而是可以尝试在草稿纸上模拟程序的执行过程。通过一步一步地推演，不仅可以加深对题目逻辑的理解，还能更直观地掌握时间复杂度的变化规律。这样做不仅有助于提高解题的准确性，还能增强同学在编程中的整体思维能力。

第二章

1
这一章同学表现得非常出色！几乎全对，展现了扎实的基础知识。数组和链表虽然是数据结构中最基本的内容，但它们的重要性不可忽视。掌握好这两个结构，不仅能帮助你更好地理解后续学习中的栈、队列、树、图等复杂的数据结构，还能为构建高效的算法打下坚实的基础。希望你在接下来的学习中继续保持这种良好的势头，把每一个知识点都掌握扎实，为应对更高难度的内容做好充分准备。继续加油;)

第三章

1
2
3
4
在解决栈和队列相关的题目时，必须仔细分析操作的顺序，这一点非常关键。具体来说，需要明确以下几点:
(1)插入元素的顺序:在某些题目中，可能要求先将元素插入到栈或队列中，然后再移动指针。这种情况下，插入操作应该优先进行。
(2)指针移动的顺序:而在另一些题目中，可能需要先移动指针到某个位置，然后再进行插入操作。在这种情况下，指针的移动操作应该先于插入操作进行。
理解并准确把握这两种不同的操作顺序，对于正确解答题目至关重要。如果操作顺序搞错了，可能会导致整个算法的错误，无法正确地解决问题。因此，在分析和编写代码时，一定要特别注意这一点。

第四章

1
2
3
4
5
6
7
8
9
题目不是很严谨
m一般小于等于n(若m>n则必定匹配不成功)
所以有0(n+m)<=0(2n)=0(n),A其实也是对的，当然单选题在有0(n+m)的情况下还是选0(n+m)好一点

KMP算法的考频一直很高，几乎每年都会出现在选择题中。虽然这些题目的难度相对适中，但要取得高分，掌握核心概念仍然至关重要。关键在于熟练掌握如何求解next和nextval数组，并理解在发生失配时，指针i和j的正确移动方式。

KMP算法的高效性在于其巧妙的匹配过程，它通过next数组记录部分匹配的信息，使得在字符串匹配过程中，避免了大量的重复比较。因此，在练习时，一定要确保对next和nextval数组的计算过程了然于心，这不仅是解题的基础，也是深入理解算法的核心。

在实际考试中，KMP题目通常不会过于复杂，只要你清楚地掌握了这些基本步骤，即使遇到失配的情况，也能够迅速调整指针位置，继续高效匹配。所以，在复习时，可以多加练习next和nextval数组的推导过程，确保自己能够熟练应对不同的题型。这样一来，面对KMP的考题时，你将能够更加自信从容。

第五章

1
2
3
4
5
6
7
卡特兰数在考研范畴内一般只会有三种应用。
(1)二叉树个数，也就是本题
(2)出栈次序
例如进栈序列为1,2,3,...n，那么一共有多少种出栈序列?
(3)括号匹配
例如n对括号可以组成多少种合法括号序列
(())是合法的，)(()是非法的。

image-20240819115711808

1
2
3
4
5
6
7
近年来408的趋势就是越来越难，体现在数据结构上就是，最开始几年代
码题都是数组和链表，而近五年考的都是树和图，这对考生们的代码能
力就提出了更高的要求。
看丁同学对这一块并不是特别熟练，我出两道题，有空的话可以做做。
用第15题的数据结构就行。
(1)将整颗二叉树进行左右翻转(每个节点的左儿子和右儿子交换)
(2)输出整颗二又树所有节点的权重和

第六章

1
2
3
4
5
6
7
8
邻接多重表和十字链表目前考频较低，但其实完全有可能出一道大题，将一个邻接多重表转为无向图，然后再在这个无向图上做文章，所以还是需要重视的。

下面一些容易混淆的概念
(强)连通图:(有)无向图中每个顶点都有路径可以到达其他任意顶点
(有向)完全图:(有)无向图中每个顶点都有边直接到达其他任意顶点
(强)连通分量:(有)无向图中的一个极大连通子图
王同学这一章做得还不错，继续加油:)
以下是我考研时总结的一些时间复杂度

image-20240729183925828

第七章

1
2
3
在学习过程中，重点把握关键概念，避免在考试中不太可能涉及的内容上花费过多时间。例如，尽管红黑树的插入删除操作都在考研大纲中，但删除操作通常被认为是边缘知识点。这个操作较为复杂，而且在历年的考试中从未考过，更大概率考的是插入操作。因此，虽然了解删除操作有益，但不需要过多深入研究。

另一方面，在学习散列表时，需要特别注意不同冲突解决方法之间的区别。尤其要牢记，在使用链地址法时，遇到空节点不算作一次查找，而在非链地址法（如开放地址法）中，空节点则算作一次查找。这一细节对于正确分析散列表操作的效率至关重要，而且更可能在考试中成为考点。继续加油:)

第八章

1
2
3
4
5
首先，恭喜雎同学顺利完成数据结构的学习阶段！接下来，你可以考虑将算法与操作系统这两门课程结合起来学习，因为它们之间有很强的关联性，可以互相补充。当然，如果你觉得合适，也可以单独开始学习计算机网络。

回到这一章的章节测试，特别是第九题，我不知道你是否有深入思考过：在堆排序中，为什么要升序排列时需要用大顶堆，而降序排列时则要用小顶堆呢？理解这些细节不仅能帮助你掌握堆排序的核心原理，还能加深你对算法设计的思考。希望这些讲解对你有帮助，继续保持良好的学习状态！

首先要明确一点，堆在计算机中是以数组的形式存储的。而堆排序每轮是将堆顶元素和堆末尾的元素进行交换，此时堆末尾的元素就是排好序的元素。因此使用大顶堆进行升序排序，每一轮正好可以将当前待排序的元素中的最大值交换到最后，属于原地排序，空间复杂度是O（1）。如果使用小顶堆进行升序排序，虽然也可以完成排序任务，但需要额外开辟一个数组，每次将堆顶元素放到这个新开辟的数组前头（如果还是与堆尾元素进行互换就是降序排序了），空间复杂度是O（n）。

操作系统

第一章

1
2
3
4
5
6
1、 CPU从特定主存地址（ROM）开始读取指令，执行ROM中的引导程序，进行硬件自检，确定磁盘位置
2、 将磁盘的第一块——主引导记录（MBR）读入内存，MBR中包含磁盘引导程序和分区表
3、 执行磁盘引导程序，从主分区（C盘）读入分区引导记录（PBR），执行其中的程序
4、 从根目录下找到找到启动管理器（操作系统初始化程序）并执行，完成开机

第一章主要介绍了一些操作系统的基础概念，其中最为关键的内容之一便是操作系统的引导过程。这部分知识不仅是理解操作系统整体工作原理的基础，更是在考试中常被考察的重点。在历年的考试真题中，操作系统的引导过程曾以大题形式出现，考察频率较高，因此对这一过程的深入理解和掌握对考试的成功至关重要。为了更好地应对考试，建议同学在学习时特别关注这部分内容，不仅要理解其理论，还要能够灵活应用于实际问题中。通过反复练习和总结，确保在考试中能够准确、清晰地描述操作系统的引导过程，以应对相关考题的要求。

第二章

1
本章核心内容相对简单，只需了解每种调度算法的基本作用即可应对考试题目。然而，对于可抢占式的调度算法，特别需要格外小心。在考试中，为了避免出错，建议画出甘特图以辅助分析。这不仅能帮助你直观地理解进程的执行顺序，还能有效减少因计算不当导致的错误。

第三章

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1、 预处理
对#include、#define等语句进行处理，预处理后仍然是高级语言

2、 编译
将高级语言编译为对应的汇编语言或机器语言（可重定位文件）

3、 汇编
将汇编语言汇编成对应的机器语言（可重定位文件）

4、 链接
将多个可重定位文件链接成一个可执行文件，确定逻辑地址

5、 装入
将可执行文件从磁盘装入内存中，确定物理地址

目前，考试中关于段表的大题出现频率较低，但我认为这是一个潜力巨大的知识点。虽然页表的考题较为常见，但段表的相关知识也不容忽视。本月王道将出版一本绿色习题册，书中涵盖了考研所有相关知识点和习题，也可以作为第二轮的复习。如果你有兴趣的话，可以留意一下这本书

第四章

1
2
3
4
5
借着第十一题,我们来搞清楚链式分配的两种方式:隐式链接和显式链接。
(1)隐式链接就像链表一样,在每个盘块最后都有指向下一个盘块的指针,我们要想访问
最后一个盘块的内容,就必须要从头开始访问所有的盘块,效率十分低下。
(2)显式链接采用FAT表存储下一个盘块号,也就是第十一题的方式。当我们知道了首个
盘块号,要想读入第五个盘块,就到FAT表里查找五次即可。

image-20240902203459857

第五章

1
在学习和复习这一章时，我们需要特别注意一些考试概念上的细节。在考研中，SCAN算法和LOOK算法通常不会被区分开来。换句话说，虽然考试题目中可能会提到SCAN或C-SCAN算法，但在回答这些题目时，同学应当按照LOOK或C-LOOK算法的原则来进行解答。

组成原理

第一章

1
2
3
4
5
6
7
8
9
10
11
12
1、 预处理
对#include、#define等语句进行处理，预处理后仍然是高级语言
2、 编译
将高级语言编译为对应的汇编语言或机器语言（可重定位文件）
3、 汇编
将汇编语言汇编成对应的机器语言（可重定位文件）
4、 链接
将多个可重定位文件链接成一个可执行文件，确定逻辑地址
5、 装入
将可执行文件从磁盘装入内存中，确定物理地址

第一章通常涵盖基本概念，并包含许多常见的缩写。在学习这些内容时，不必过于执着于死记硬背每一个概念对应的公式。更为重要的是，理解这些概念背后的意义和原理。当你真正理解了这些概念，它们的公式和应用便会自然而然地浮现在脑海中，成为你思维的一部分。通过这样的学习方式，你不仅能够灵活运用这些公式，还能够更深入地掌握这些概念之间的联系，进而提升对整个知识体系的理解与运用能力。

第二章

1
这一章的重点在于掌握IEEE浮点数表示的格式，这是考试中经常出现的考点，几乎每年都会有相关的选择题。特别要注意的是，特殊情况的表示方式以及短浮点数和长浮点数的格式区别，这些细节在考试中往往是出题的关键。为了帮助大家更好地理解和记忆这些内容，我专门整理了两张表格，供大家参考和复习。

image-20240813224203690

第三章

1
2
3
4
5
6
7
8
9
10
这里需要稍微注意的是，虽然考试中很少涉及全相联映射的考题，但实际上，全相联映射是组相联映射的一种特殊情况——它的组数为1。因此，全相联映射的计算方法与组相联映射是一致的。

假设我们使用全相联映射，已知内存块大小为16B，Cache容量为32KB，内存总容量为4MB。那么具体的计算结果如下：
标记位：标记位的计算与内存地址和缓存块的数量有关。这里内存容量为4MB，共计2^22B，而Cache容量一共为2^15B,因此标记位就为位

比较器：Cache容量为32KB，单个内存块16B，因此Cache中可以容纳 32×1024/16=2048个块。这意味着需要2048个比较器来进行标记匹配。

算法位：算法位数的计算基于内存块大小。这里内存块为16B，因此算法位为低4位。因为Cache容量为32KB，Cache中有2048个块，因此需要11位来区分这些块。

因此，在这种配置下，标记位为9位，需要2048个比较器，算法位为11位。了解这些计算方法和原理，有助于更深入地理解缓存映射的工作机制。

第四章

1
2
3
这一章在计算机组成原理中既是难点，也是考试的重点，大题几乎每年都会考察。在复习过程中，需要特别注意Inter和AT&T格式的区别，尤其是目的操作数和源操作数的位置顺序问题，搞清楚到底是哪个在前，哪个在后。

本章中的读代码题相对来说难度较高，题目中并不会给出明确的提示。不过，真题往往会通过前几个小问的设置为后续大题提供一些线索，提示考生这段代码的功能。因此，栗同学也不必过于担心，只要仔细分析前面的提示信息，并在复习中多加练习，就能够应对这类题目。继续保持信心，好好加油！

第五章

1
这一章可以说是计算机组成原理中最为复杂的一章，要求同学对指令执行过程有深入的理解。比如，在指令执行的过程中，同学需要明确何时进行访存操作，何时程序计数器（PC）递增等。这些知识点经常出现在大题中，成为考察同学掌握程度的重要内容。同学在学习过程中可以尝试将指令执行的过程图示化，将每个步骤以流程图的形式绘制出来，标注出在每一步中发生的具体操作，图示化的学习可以帮助你更直观地理解抽象概念。

第六章

1
2
3
4
5
6
7
这一章的内容虽然相对基础，但要求我们在审题时特别细致，尤其是在涉及多模块存储器的部分。多模块存储器的存取方式主要有两种：轮流启动和同时启动。本章的大题重点探讨的是轮流启动的方式，但同时启动的方式也是非常重要的。

轮流启动的方式 是一种有效的存取方法，通过依次对各个存储模块进行操作，减少了存取冲突，从而提升了系统的整体效率。每个存储模块按照预定的顺序被启动，这样在一个模块处理数据时，其他模块可以准备好下一步的操作，从而最大化利用系统资源。

同时启动的方式 则是另一种策略，在这种方式下，多个存储模块可以同时被启动并进行数据处理。这种方式的优点在于它可以大幅度提高数据吞吐量，适用于需要高并发操作的场景。然而，它对系统的设计要求更高，因为需要确保各个模块之间的协调和同步，避免资源竞争和数据冲突。

理解这两种存取方式不仅有助于解题，更能帮助你在实际应用中选择最合适的方案。因此，在学习和应用过程中，细致审题并掌握每种方式的优劣，是非常关键的。

image-20240830095337623

第七章

1
2
3
4
5
6
7
8
9
I/O设备这一章的学习重点主要包括以下几个方面：

三种数据传输方式：这部分内容是考试的高频考点，曾经出现在真题中的一道完整的大题中，考察了考生对查询方式、中断方式和DMA方式的理解与应用。

I/O接口与I/O端口的区别：弄清楚这两者的差异对于理解计算机系统的硬件结构至关重要，明确它们在数据传输与设备通信中的不同角色。

哪些设备属于I/O接口：辨别哪些设备属于I/O接口范畴是理解系统架构的基础，掌握这一点可以帮助理清计算机系统中各硬件组件的功能和作用。

这些内容是学习I/O设备时需要重点掌握的知识点，充分理解并应用这些概念对于应对考试和实际操作都有重要意义。

计网

第一章

1
计算机网络这门课相对来说是四门专业课中比较简单的一门，不过其中需要记忆的知识点仍然不少，尤其是一些计算公式和概念。当前咸鱼更新仅到第三章，进度相对较慢。如果有同学想继续学习后续章节的内容，推荐后续章节同学可以观看b站湖科大的视频，是湖科大的高老师讲的。高老师的授课内容条理清晰，逻辑严谨，能够帮助大家更好地理解这门课程的核心知识点。对于需要掌握的重点内容和复杂概念，视频中的讲解也十分到位。

第二章

1
2
3
4
5
6
7
8
9
10
11
12
13
14
关于以太网传输标准，给同学总结一下，因为考试可能并不会告诉同学具体的信息，而会直接采用100BaseT这种代号的形式。
100BaseT 是一种以太网标准，属于 IEEE 802.3 标准族中的一种，通常用于局域网。

100：表示其数据传输速率为 100 Mbps。
Base：代表基带传输，即所有的网络带宽都用于以太网信号，而不用于其他信号类型（例如模拟信号）。
T：指的是双绞线，即使用双绞线电缆作为物理介质进行数据传输。

Base：基带传输
T：双绞线
F：光纤
L：长距离
S：短距离
E：扩展距离
W：广域网

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 672 阅读时长 ≈ 1 分钟

Amadeus

一、执行流程

  1. 语音转文本：

    • 语音情绪识别：emotion2vec
    • 语音识别：Whisper

  2. 聊天交互：Qwen2

  3. 文本转语音：

    • 文本情绪识别：BERT
    • 语音生成：GPT-SoVITS

  4. 表现形式：2d/3d模型

一、 VITS

1. VAE

VAE 模型基本原理简单介绍_smile-yan的博客-CSDN博客_vae模型

  • KL 散度

当我们想使用简单分布近似所观测到的数据分布时，KL 散度可以用于衡量在近似的过程中损失了多少信息。因此我们可以使用 KL 散度作为损失函数，从而学习到复杂数据的近似分布。
$$
D_{KL}(p||q) = \sum^N_{i=1}p(x_i)(logp(x_i)-logq(x_i))
$$
==KL 散度不能用于衡量两个分布之间的距离，因为 KL 散度不是对称的 （$$D_{KL}(p||q) != D_{KL}(q||p)$$）==

  • 损失函数

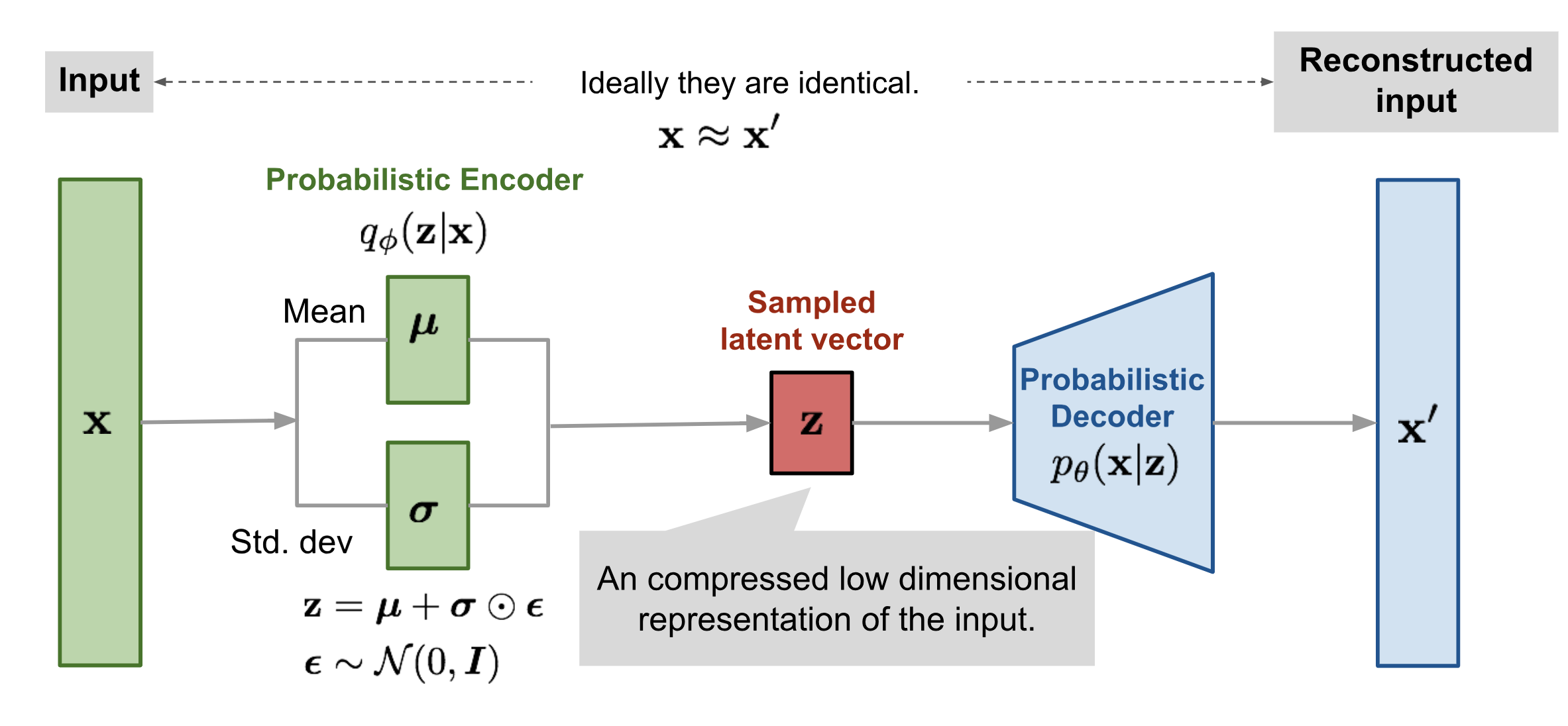
$$
L(θ,φ;x,z) = E_{z \sim q_φ(x|z)[logp_θ(x|z)]} + D_{KL}(q_φ(z|x)||p(z))\
L(θ,φ;x,z) = E_q[log(Decoder的输出分布)] + D_{KL}(Encoder的输出分布||预设的正太分布)\
L(θ,φ;x,z) = \frac{1}{m}\sum^m_{i=1}(x_i-\hat{x_i})^2 + D_{KL}(q_φ(z|x)||p(z))
$$

后半部分的KL 散度控制 Encoder 输出类正太分布，而前半部分的期望则是重构损失，用于衡量输入与输出的差异。在实际的代码编写中，一般使用MSE代替左半部分。

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 2.4k 阅读时长 ≈ 4 分钟

一、Overview

[Kaggle竞赛地址](ML2021Spring-hw2 | Kaggle)

竞赛内容：根据声音 frame 预测 phoneme 的类别（39分类问题）

训练数据格式：1229932 × 429，此处将前后五个frame连接在一起，可以更好地预测当前的类别

测试数据格式：451552 × 429

二、Strong Baseline

暂时没有过 StrongBaseline

  • 训练集重采样

    训练集类别之间数量差异极大，类别最高的数量可达178713，而最低的类别只有3883。在验证集上验证时这些低数据量的类别预测率普遍低于高数据量的样本，这里将每个类别数量都拓展到15000。修改后低数据量类别预测率显著提高，但总体预测率并未有明显提高，可能测试集中的低数据量类别的样本也同样少。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    train_class = []
    class_idx = np.arange(train_x.shape[0])
    for i in range(39):
        train_class.append(class_idx[train_y == str(i)])

    min_num = 15000
    for i in range(39):
        addition = min_num - vote[str(i)]
        if addition <= 0:
            continue
        print(i, addition)
        idx = np.random.choice(train_class[i], addition)
        train_x = np.vstack([train_x, train_x[idx]])
        train_y = np.append(train_y, train_y[idx])

  • 增大网络模型

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    class Classifier1(nn.Module):
        def __init__(self):
            super(Classifier1, self).__init__()
            self.dropout = nn.Dropout(0.5)
            
            self.layer1 = nn.Linear(429, 2048)
            self.layer2 = nn.Linear(2048, 2048)
            self.layer3 = nn.Linear(2048, 2048)
            self.layer4 = nn.Linear(2048, 1024)
            self.layer5 = nn.Linear(1024, 512)
            self.layer6 = nn.Linear(512, 128)
            
            self.BatchNorm0 = nn.BatchNorm1d(429)
            self.BatchNorm1 = nn.BatchNorm1d(2048)
            self.BatchNorm2 = nn.BatchNorm1d(2048)
            self.BatchNorm3 = nn.BatchNorm1d(2048)
            self.BatchNorm4 = nn.BatchNorm1d(1024)
            self.BatchNorm5 = nn.BatchNorm1d(512)
            self.BatchNorm6 = nn.BatchNorm1d(128)
            
            self.out = nn.Linear(128, 39)
            self.act_fn = nn.LeakyReLU()

        def forward(self, x):
            x = self.BatchNorm0(x)
            
            x = self.layer1(x)
            x = self.act_fn(x)
            x = self.BatchNorm1(x)
            x = self.dropout(x)

            x = self.layer2(x)
            x = self.act_fn(x)
            x = self.BatchNorm2(x)
            x = self.dropout(x)

            x = self.layer3(x)
            x = self.act_fn(x)
            x = self.BatchNorm3(x)
            x = self.dropout(x)
            
            x = self.layer4(x)
            x = self.act_fn(x)
            x = self.BatchNorm4(x)
            x = self.dropout(x)
            
            x = self.layer5(x)
            x = self.act_fn(x)
            x = self.BatchNorm5(x)
            x = self.dropout(x)
            
            x = self.layer6(x)
            x = self.act_fn(x)
            x = self.BatchNorm6(x)
            x = self.dropout(x)

            x = self.out(x)
            
            return x

  • 使用l2正则

1
2
# l2正则即在loss中添加|w|^2,控制w的大小,求导后本质上等同于weight_decay
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=1e-4)

  • 后处理（提升明显）

    音频信号是连续的，而frame的长度只有25ms，因此一个单词往往会对应多个frame，这些frame都是连续的且类别相同。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    # 11 3 11 -> 11 11 11
    count = 0
    for i in range(1, len(predict)-1):
        previous_ = predict[i-1]
        next_ = predict[i+1]
        current_ = predict[i]
        if (previous_ != current_) and (next_ != current_) and (previous_ == next_):
            predict[i] = previous_
            count +=1

    print('total number of correction %d, correction percent %.2f'% (count, count/len(predict)))

    image

猜测要使用lstm，gru等语言类模型或训练多个模型进行ensemble