紫梦沁香
0%

算法（第4版）读书笔记

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 14k 阅读时长 ≈ 25 分钟

数据结构实现

完整的栈实现

记得刚学 java 的时候就有实现过一个 stack，当然那时写代码不会考虑那么多，这一次添加了泛型和数组扩容，提高了可扩展性，还实现了 Iterable 可迭代接口，这样 MyStack 类就可以使用 foreach 循环了。

另外，由于 Java 的垃圾收集策略是回收所有无法被访问的对象的内存，而但我们进行 pop 操作时，虽然使用者已经不可能再访问这个被弹出的元素了，但是它的引用还存在与数组之中，因此 Java 的垃圾收集器并不会去回收这个元素！！！除非后续将该引用覆盖。即使用例已经不再需要这个元素了，数组中的引用仍然可以让它继续存在，这种情况（保存一个不需要的对象的引用）就被称作游离。一般可以通过显式使用 null 来覆盖不需要的对象即可（见37行）！

栈的数组实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class MyStack<T> implements Iterable<T>{
    private int count = 0;
    private T[] arr;

    public MyStack() {
        this(10);   // 给予有参构造函数默认参数
    }

    public MyStack(int size) {
        arr = (T[]) new Object[size];   // java不支持泛型数组，只能强转或是使用集合类型
    }

    public boolean isFull(){
        return arr.length == count;
    }

    public boolean isEmpty(){
        return count == 0;
    }

    public int size(){
        return count;
    }

    public void push(T item){
        if (isFull()){
            resizingArray(count * 2);
        }
        arr[count++] = item;
    }

    public T pop(){
        if (isEmpty()){
            throw new ArrayIndexOutOfBoundsException();
        }
        T item = arr[--count];
        arr[count] = null;  // 解决游离问题
        if(count == arr.length / 4){  // 保证数组的使用率始终大于1/4
            resizingArray(arr.length / 2);
        }
        return item;
    }

    // 更改数组大小
    public void resizingArray(int size){
        T[] newArr = (T[]) new Object[size];
        for(int i=0;i<count;i++){
            newArr[i] = arr[i];
        }
        arr = newArr;
    }

    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            int i = count;
            @Override
            public boolean hasNext() {
                return i > 0;
            }

            @Override
            public T next() {
                return arr[--i];
            }
        };
    }
}

栈的链表实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class MyLinkedStack<T> implements Iterable<T>{
    private Node head;
    private int count;

    public MyLinkedStack() {
        head = new Node();
        count = 0;
    }

    public boolean isEmpty(){
        return head.next == null;
    }

    public void push(T item){
        Node node = new Node();
        node.item = item;
        node.next = head.next;
        head.next = node;
        count++;
    }

    public T peek(){
        if (isEmpty()){
            return null;
        }
        return head.next.item;
    }

    public T pop(){
        if (isEmpty()){
            throw new ArrayIndexOutOfBoundsException("栈空！！！");
        }
        T item = head.next.item;
        head.next = head.next.next;
        count--;
        return item;
    }

    public int size(){
        return count;
    }

    @Override
    // 区别于数组实现的迭代器
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node tmp = head;
            @Override
            public boolean hasNext() {
                return tmp.next != null;
            }

            @Override
            public T next() {
                tmp = tmp.next;
                return tmp.item;
            }
        };
    }
	
    // 私有内部类 Node，可以直接使用外部的泛型类型！！！
    private class Node{
        Node next;
        T item;
    }
}

算法实现

并查集

先定义算法的 api

1
2
3
4
5
6
7
8
9
10
public interface IUnionFind {
    // 连接两点
    void union(int p, int q);
    // 查找某点的根节点
    int find(int p);
    // 返回两点是否连接
    boolean connected(int p, int q);
    // 返回连通分量的个数
    int count();
}

QuickFind，快速查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class QuickFind implements IUnionFind{
    private int[] links;
    private int count;

    public QuickFind(int num) {
        links = new int[num];
        for(int i=0;i<num;i++){
            links[i] = i;
        }
        count = num;
    }

    @Override
    public int find(int p){
        return links[p];
    }

    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public int count() {
        return count;
    }

    @Override
    public void union(int p, int q){
        int pID = find(p);
        int qID = find(q);
        if (pID == qID){
            return;
        }

        for(int i=0;i<links.length;i++){
            if(pID == links[i]){
                links[i] = qID;
            }
        }
        count--;
    }
}

上述代码，虽说查询根节点速度很快，但由于连接的时候需要将所有的连通节点都改为同一个根节点，因此效率很差。

QuickUnion，快速合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class QuickUnion implements IUnionFind{
    private int count;
    private int[] links;

    public QuickUnion(int num) {
        count = num;
        links = new int[num];
        for(int i=0;i<num;i++){
            links[i] = i;
        }
    }

    @Override
    public void union(int p, int q) {
        if (connected(p, q)){
            return;
        }
        int pID = find(p);
        int qID = find(q);
        links[qID] = pID;
        count--;
    }

    @Override
    public int find(int p) {
        while(links[p] != p){
            p = links[p];
        }
        return p;
    }

    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public int count() {
        return count;
    }
}

而 QuickUnion 在连接的时候只修改根节点的值，解决了连接速度慢的问题。取而代之的是，在查找的时候不能直接返回某点的根节点了。

WeightedQuickUnion，加权快速合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class WeightedQuickUnion implements IUnionFind{
    private int count;
    private int[] links;
    private int[] weights;

    public WeightedQuickUnion(int num) {
        count = num;
        links = new int[num];
        weights = new int[num];
        for(int i=0;i<num;i++){
            links[i] = i;
            weights[i] =1;
        }
    }

    @Override
    public void union(int p, int q) {
        if (connected(p, q)){
            return;
        }
        int pID = find(p);
        int qID = find(q);
        if(weights[pID] < weights[qID]){
            weights[qID] += weights[pID];
            links[pID] = qID;
        }else{
            weights[pID] += weights[qID];
            links[qID] = pID;
        }
        count--;
    }

    @Override
    public int find(int p) {
        while(links[p] != p){
            p = links[p];
        }
        return p;
    }

    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public int count() {
        return count;
    }
}

QuickUnion 最坏情况下会像有序数组生成二叉排序树那样，变成类似链表的数据结构，这会大大降低查询和连接的速度，而 WeightedQuickUnion 通过将小树连接到大树解决了这个问题！

PathCompressedWeightedQuickUnion，路径压缩的加权快速合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class PathCompressedWeightedQuickUnion implements IUnionFind{
    private int count;
    private int[] links;
    private int[] weights;

    public PathCompressedWeightedQuickUnion(int num) {
        count = num;
        links = new int[num];
        weights = new int[num];
        for(int i=0;i<num;i++){
            links[i] = i;
            weights[i] =1;
        }
    }

    @Override
    public void union(int p, int q) {
        if (connected(p, q)){
            return;
        }
        int pID = find(p);
        int qID = find(q);
        if(weights[pID] < weights[qID]){
            weights[qID] += weights[pID];
            links[pID] = qID;
        }else{
            weights[pID] += weights[qID];
            links[qID] = pID;
        }
        count--;
    }

    @Override
    public int find(int p) {
        while(links[p] != p){
            return links[p] = find(links[p]);
        }
        return p;
    }

    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public int count() {
        return count;
    }
}

上诉代码，在查询根节点的过程中，通过递归将所有子节点的父节点直接修改为了根节点，将整棵树的高度锁定在了2！

效率对比

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class EfficiencyTest {
    public static void main(String[] args) {
        Scanner sc1 = FileUtils.getFileScanner("tinyUF.txt");
        Scanner sc2 = FileUtils.getFileScanner("tinyUF.txt");
        Scanner sc3 = FileUtils.getFileScanner("tinyUF.txt");
        Scanner sc4 = FileUtils.getFileScanner("tinyUF.txt");
        QuickFind uf1 = new QuickFind(sc1.nextInt());
        QuickFind uf2 = new QuickFind(sc2.nextInt());
        QuickFind uf3 = new QuickFind(sc3.nextInt());
        QuickFind uf4 = new QuickFind(sc4.nextInt());
        System.out.println("==============================tiny==============================");
        System.out.println("QuickFind:" + test(uf1, sc1) + "ms" + "\n" + "components: " + uf1.count());
        System.out.println("QuickUnion:" + test(uf2, sc2) + "ms" + "\n" + "components: " + uf2.count());
        System.out.println("WeightedQuickUnion:" + test(uf3, sc3) + "ms" + "\n" + "components: " + uf3.count());
        System.out.println("PathCompressedWeightedQuickUnion:" + test(uf4, sc4) + "ms" + "\n" + "components: " + uf4.count());
        System.out.println("==============================medium==============================");
        sc1 = FileUtils.getFileScanner("mediumUF.txt");
        sc2 = FileUtils.getFileScanner("mediumUF.txt");
        sc3 = FileUtils.getFileScanner("mediumUF.txt");
        sc4 = FileUtils.getFileScanner("mediumUF.txt");
        uf1 = new QuickFind(sc1.nextInt());
        uf2 = new QuickFind(sc2.nextInt());
        uf3 = new QuickFind(sc3.nextInt());
        uf4 = new QuickFind(sc4.nextInt());
        System.out.println("QuickFind:" + test(uf1, sc1) + "ms" + "\n" + "components: " + uf1.count());
        System.out.println("QuickUnion:" + test(uf2, sc2) + "ms" + "\n" + "components: " + uf2.count());
        System.out.println("WeightedQuickUnion:" + test(uf3, sc3) + "ms" + "\n" + "components: " + uf3.count());
        System.out.println("PathCompressedWeightedQuickUnion:" + test(uf4, sc4) + "ms" + "\n" + "components: " + uf4.count());
        System.out.println("==============================large==============================");
        // 其余三个速度太慢，这里就不测试了
        sc4 = FileUtils.getFileScanner("largeUF.txt");
        uf4 = new QuickFind(sc4.nextInt());
        System.out.println("PathCompressedWeightedQuickUnion:" + test(uf4, sc4) + "ms" + "\n" + "components: " + uf4.count());

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
==============================tiny==============================
QuickFind:0ms
components: 2
QuickUnion:0ms
components: 2
WeightedQuickUnion:1ms
components: 2
PathCompressedWeightedQuickUnion:2ms
components: 2
==============================medium==============================
QuickFind:17ms
components: 3
QuickUnion:11ms
components: 3
WeightedQuickUnion:6ms
components: 3
PathCompressedWeightedQuickUnion:4ms
components: 3
==============================large==============================
PathCompressedWeightedQuickUnion:798220ms
components: 6

Process finished with exit code 0

可以发现，在 tiny 小数据集上，最优的那个算法反而最慢，但当数据量慢慢增大时，它的优势就显现出来了。

排序算法

排序工具类

在实现各种排序算法的过程中，不免会使用一些基础的操作（交换，比较等），这里就单独封装在一个排序的工具类中了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class SortUtil {
    public static boolean less(Comparable a, Comparable b) {
        return a.compareTo(b) < 0;
    }

    public static void swap(Comparable[] arr, int i, int j) {
        if (i == j) {
            return;
        }
        Comparable tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    public static void show(Comparable[] arr) {
        for (Comparable comparable : arr) {
            System.out.print(comparable + " ");
        }
        System.out.println();
    }

    public static boolean isSorted(Comparable[] arr) {
        for (int i = arr.length - 1; i >= 1; i--) {
            if (less(arr[i], arr[i - 1])) {
                return false;
            }
        }
        return true;
    }
}

选择排序

一种最简单的排序算法是这样的:首先，找到数组中最小的那个元素，其次，将它和数组的第一个元素交换位置（如果第一个元素就是最小元素那么它就和自己交换）。再次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。这种方法叫做选择排序，因为它在不断地选择剩余元素之中的最小者。

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Selection {
    public static void sort(Comparable[] arr) {
        for (int i = 0; i < arr.length-1; i++) {
            int min = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (SortUtil.less(arr[j], arr[min])) {
                    min = j;
                }
            }
            SortUtil.swap(arr, i, min);
        }
    }
}

对于长度为 N 的数组，选择排序需要 ~$\frac{N^2}{2}$ 次比较以及 ~$N$ 次交换。

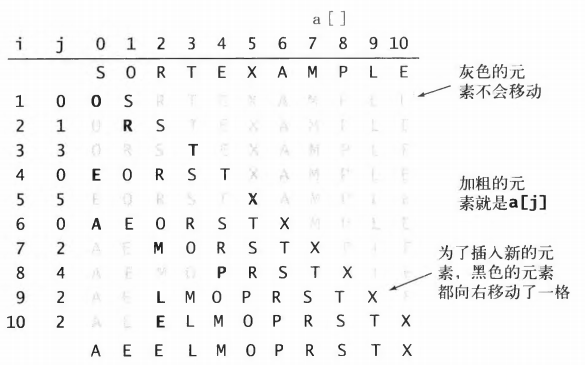
插入排序

通常人们整理桥牌的方法是一张一张的来,将每一张牌插入到其他已经有序的牌中的适当位置。在计算机的实现中，为了给要插入的元素腾出空间，我们需要将其余所有元素在插入之前都向右移动一位。这种算法被称作插入排序。

1
2
3
4
5
6
7
8
9
10
11
public class Insertion {
    public static void sort(Comparable[] arr) {
        for(int i=1;i< arr.length;i++){
            for (int j=i;j>0;j--){
                if (SortUtil.less(arr[j], arr[j-1])){
                    SortUtil.swap(arr, j, j-1);
                }
            }
        }
    }
}

对于长度为 N 的数组，插入排序平均需要进行 ~$\frac{N^2}{4}$ 次比较以及 ~$\frac{N^2}{4}$ 次交换，最好情况下需要进行 N-1 次比较以及0次交换，而在最坏情况下，需要进行 ~$\frac{N^2}{2}$ 次比较以及 ~$\frac{N^2}{2}$ 次交换（即对角线下方元素都需要进行交换与比较）。

image

与选择排序一样，当前索引左边的所有元素都是有序的，但它们的最终位置还不确定，为了给更小的元素腾出空间，它们可能会被移动。但是当索引到达数组的右端时，数组排序就完成了。
和选择排序不同的是，插入排序所需的时间取决于输入中元素的初始顺序。例如，对一个很大且其中的元素已经有序（或接近有序）的数组进行排序将会比对随机顺序的数组或是逆序数组进行排序要快得多。


插入排序（修改）

要大幅提高插人排序的速度并不难，只需要在内循环中将较大的元素都向右移动而不总是交换

两个元素（这样访问数组的次数就能减半）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static void sortByMoving(Comparable[] arr) {
        for (int i = 1; i < arr.length; i++) {
            Comparable tmp = arr[i];
            int j = i - 1;
            for (; j >= 0; j--) {
                if (SortUtil.less(tmp, arr[j])) {
                    arr[j + 1] = arr[j];
                } else {
                    break;
                }
            }
            arr[j + 1] = tmp;
        }
    }

希尔排序

希尔排序一种基于插人排序的快速的排序算法。对于大规模乱序数组插入排序很慢，因为它只会交换相邻的元素，因此元素只能一点一点地从数组 的一端移动到另一端。例如，如果主键最小的元素正好在数组的尽头，要将它挪到正确的位置就需要 N-1 次移动。希尔排序为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。

希尔排序的思想是使数组中任意间隔为 h 的元素都是有序的。这样的数组被称为 h 有序数组。换句话说，一个 h 有序数组就是 h 个互相独立的有序数组编织在一起组成的一个数组。在进行排序时，如果 h 很大，我们就能将元素移动到很远的地方，为实现更小的 h 有序创造方便。用这种方式，对于任意以1结尾的 h 序列，我们都能够将数组排序。这就是希尔排序。

image

下面算法实现使用了序列 $3n+1$，从N/3开始递减至1。我们把这个序列称为递增序列。一种方式是实时计算它的递增序列，另—种方式则是将递增序列存储在一个数组中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void sort(Comparable[] arr) {
    int n = arr.length;
    // 计算序列第一项
    int h = 1;
    while (h < n / 3) {
        h = h * 3 + 1;  // 1, 4, 13, 40, 121...
    }

    while (h > 0) {
        for (int i = h; i < n; i++) {
            Comparable tmp = arr[i];
            int j = i;
            for (; j >= h; j -= h) {
                if (SortUtil.less(tmp, arr[j - h])) {
                    arr[j] = arr[j - h];
                }else {
                    break;
                }
            }
            arr[j] = tmp;
        }
        h = (h - 1) / 3;
    }
}

至于上述希尔排序的性能（根据 h 序列的取值，排序的时间复杂度会有所不同）， 目前最重要的结论是它的运行时间达不到平方级别。

不过，已知在最坏的情况下比较次数和 $N^{3/2}$ 成正比。

神奇的用法

不会报错的除零运算

下述代码并不会像1 / 0 一样报除零异常，而是会返回 Infinity

1
2
3
4
public void test2(){
    System.out.println(1.0 / 0.0);	// Infinity
    System.out.println(1.0 / 0.0 > 1e9); // true
}

可以“修改”的 final 变量

被 final 所修饰的变量无法被修改，下述代码中 arr 是 final 变量，因此在第5行想给它赋予一个新的值时报错了： **Cannot assign a value to final variable ‘arr’**。

虽然实例变量的值无法被修改，但是对象的值本身是可以被修改的（请看第4行）！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class MyTest {
    public static void main(String[] args) {
        A a = new A();
        a.arr[0] = 20;
        // a.arr = new int[10]; Cannot assign a value to final variable 'arr'
        System.out.println(a.arr[0]);
    }
}

class A {
    // 常量arr
    final int[] arr;
    
    public A(){
        this.arr = new int[10];
    }
}

巧妙压缩日期格式

常规方法，使用三个变量来分别存储年月日。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class MyDate{
    int day;	// 日
    int month;	// 月
    int year;	// 年
    
    public MyDate(int year, int month, int day) {
        this.day = day;
        this.month = month;
        this.year = year;
    }
    
    @Override
    public String toString() {
        return "现在是" + year + "年" + month + "月" + day + "日";
    }
}

压缩方法，只使用一个变量来存储年月日。

年月日我们可以把它转换为特殊进制的数 YMD，这个特殊进制每一位的权重并不相同，由于一个月最多有31天，一年有12月，因此 D 是32进制的，而 M 是13进制的，Y 则没有进制，可以一直往上加。

举个例子，假设是 x 年 y 月 z 日，那么 YMD 就应该等于 z + 32 * y + 32 * 13 * x。

当然，这个 YMD 只能算是压缩，是不可能用于最后输出的（毕竟别人不知道这是特殊进制），因此还需要解压。

根据 date = z + 32 * y + 32 * 13 * x，易得 x = date / 416，z = date % 32，而 y 可以先求出一共有多少月 months = date / 32，然后再通过 months % 13 就能算出来 y 了！

1
2
3
4
5
6
7
8
9
10
11
12
class MyDateCompressed{
    int date;

    public MyDateCompressed(int year, int month, int day) {
        date = day + 32 * month + 416 * year;
    }

    @Override
    public String toString() {
        return "现在是" + date / 416 + "年" + date / 32 % 13 + "月" + date % 32 + "日";
    }
}