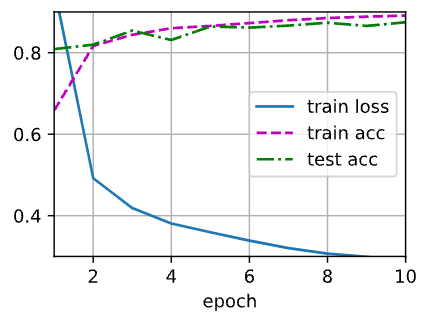
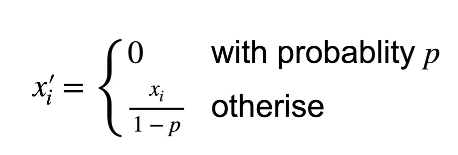在训练模型的过程中,过拟合几乎是不可避免的。因此可以这么说,深度学习就是训练一个庞大的模型,在此基础上我们来降低过拟合的程度。相较之下,如果模型欠拟合了,貌似除了扩大模型就没有任何方法了。
下面介绍几个常用的降低过拟合的方法。
一、正则化
1. 什么是正则化?
正则化的思想,即通过限制参数值的选择范围来控制模型容量。而正则化又分为岭回归(权重衰退)、LASSO 回归和弹性网络等。下面我着重说明的是岭回归。
首先,先来看一张极度过拟合的图像。
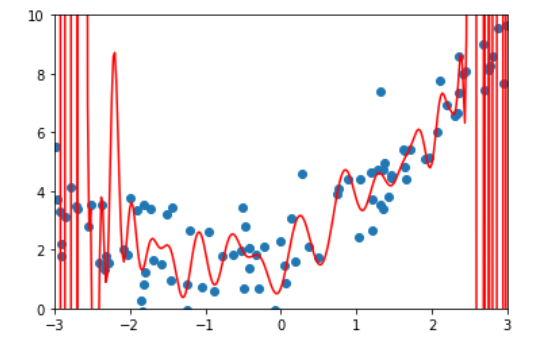
这是上述图像的部分权重,无一例外,每个 $W_i$ 都极其的大,这也导致了图像十分的陡峭。
1
2
3
4
5
6
7
| array([-4.09493627e+11, 5.76349998e+12, 1.71369179e+11, -9.99031499e+12,
9.23500127e+11, 9.26094018e+12, -1.94635409e+12, -5.40895631e+10,
7.94601628e+11, -7.85418293e+12, 1.63904594e+12, 1.67984971e+12,
-9.87156668e+11, 6.88721582e+12, -1.64914180e+12, 3.50775793e+11,
2.60751888e+11, -5.87372086e+12, 1.66748622e+12, -3.77434047e+12,
1.00605169e+12, 2.34190394e+12, -8.57867266e+11, 5.39077331e+12,
-1.60621032e+12, 2.95930952e+12, -9.52432067e+11, -1.74889800e+12])
|
因此很自然而然地就能想到,那我限制 $W_i$ 的选择范围就行了嘛。从模型的角度来说,参数数量不变,但参数的选择范围小了,那模型自然也变小了。
于是就有了使用均方范数作为硬性限制,小的 θ 意味着更强的正则项。
需要注意的是,偏置 b 并没有加入到正则化中来,毕竟我们的目标是让曲线更加的平缓,跟偏置 b 没有什么关系。
$min l(w,b) \quad subject\ to \quad ||W||^2 \le θ,\quad\quad ||W||^2 = \sum W^2$
但硬性限制优化求导比较麻烦,结果也会比较硬,一般使用均方范数作为柔性限制。
$loss = l(w, b) + \frac{λ}{2}||W||^2$
其中超参数 λ 控制了正则项的重要程度
- λ = 0,即无正则化,和普通的损失函数没有区别。
- λ → $\infty$,此时 W → 0
2. 如何影响损失函数?
可以看到,原先的极值点 $\widetilde{W}^*$ 在绿色椭圆的圆心,但在加入正则化项之后,极值点在两者之间做了一个权衡,取在了切点。
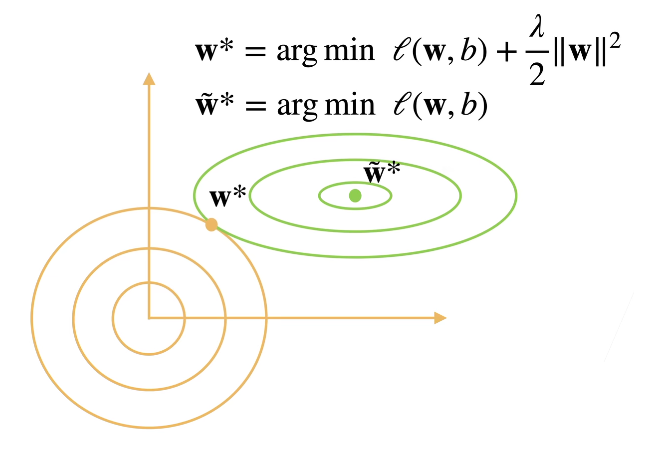
3. 参数更新法则
计算梯度
$\frac{\partial}{\partial W}(l(W, b) + \frac{λ}{2}||W||^2) = \frac{\partial l(W, b)}{\partial W} + λW$
更新参数
$W’ = W - η(\frac{\partial l(W, b)}{\partial W} + λW) = (1 - ηλ)W - η\frac{\partial l(W, b)}{\partial W}$
通常 ηλ < 1,因此每次在参数更新时,都会对 W 进行缩小,也就是权重衰退这个名字的由来。
4. 岭回归
1
2
3
4
5
6
7
| def RidgeRegression(degree,alpha):
pipeline = Pipeline([
("poly",PolynomialFeatures(degree = degree)),
("std_scaler",StandardScaler()),
("ridge_reg",Ridge(alpha=alpha))
])
return pipeline
|
alpha = 0,即普通多项式回归。
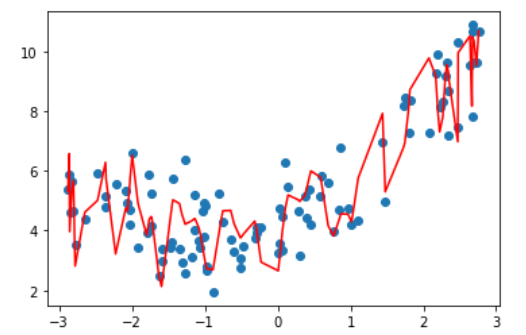
alpha = 1e-4,曲线一下子就柔和了。
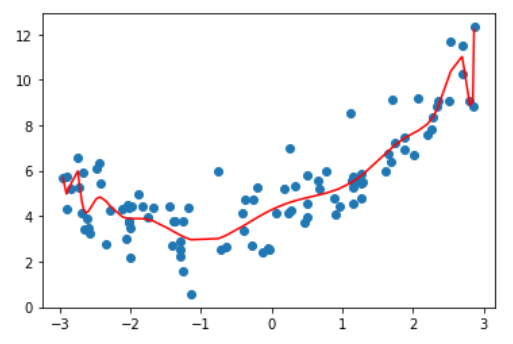
alpha = 100,有点像二次曲线了。

alpha → $\infty$,为了控制损失函数,只能将权重设为0。
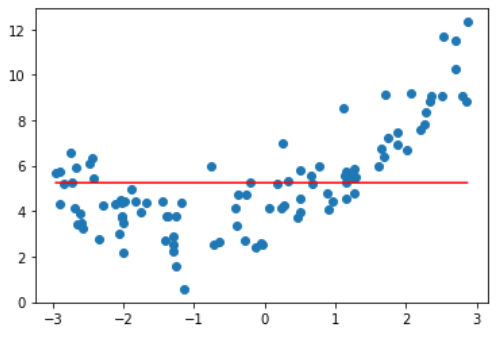
5. Tensorflow 岭回归实现
为了能够过拟合,只设置了20个训练样本,每个样本有 200 个特征。
1
2
3
4
5
6
7
8
9
10
11
| n_train = 20
n_test = 100
num_inputs = 200
batch_size = 5
num_outputs = 1
true_w, true_b = tf.ones([num_inputs, 1]) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
train_iter = d2l.load_array(train_data, batch_size)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
|
参数初始化,线性模型没那么多讲究,初始化为0也行。
1
2
3
4
5
6
| def init_params(num_inputs, num_outputs):
W = tf.Variable(tf.random.normal(mean=1, shape=(num_inputs, 1)))
b = tf.Variable(tf.zeros(num_outputs))
return [W, b]
W, b = init_params(num_inputs, num_outputs)
|
网络模型
1
2
3
4
5
6
7
8
9
10
11
|
def net(X):
return X @ W + b
def l2_penalty(W):
return tf.reduce_sum(tf.pow(W, 2)) / 2
def loss(y, y_hat):
return tf.reduce_mean(tf.square(y - y_hat))
|
训练函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def train(lambd, epochs = 100, lr = 0.003):
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, epochs], legend=['train', 'test'])
for epoch in range(epochs):
for X, y in train_iter:
with tf.GradientTape() as tape:
l = loss(y, net(X)) + lambd * l2_penalty(W)
grads = tape.gradient(l, [W, b])
for param, grad in zip([W, b], grads):
param.assign_sub(grad * lr)
if (epoch + 1) % 5 == 0:
animator.add(epoch +1, (d2l.evaluate_loss(net, train_iter, loss),
(d2l.evaluate_loss(net, test_iter, loss))))
print("W的L2范数是", tf.norm(W).numpy())
|
train(lambd = 0)
模型没有泛化,光是训练误差减小,典型的过拟合。
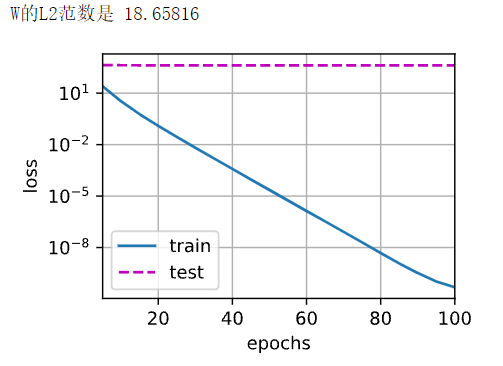
train(lambd = 3)
训练和测试误差都在同步降低,且两者差距较上述过拟合之下减小了不少。
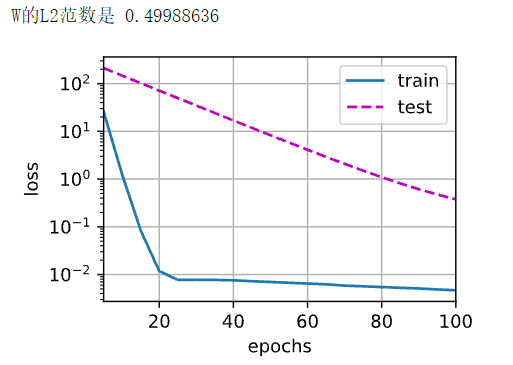
train(lambd = 20)
同上,效果更好了。
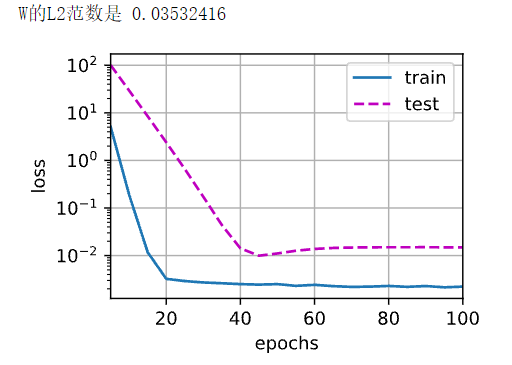
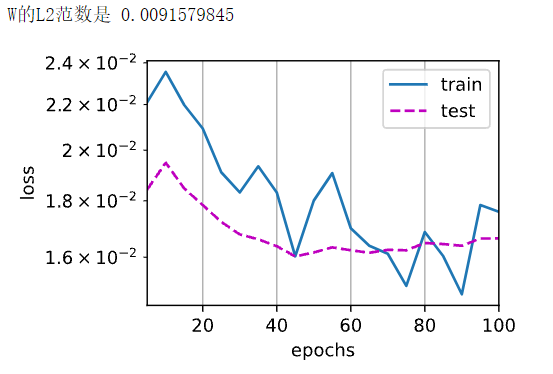
train(lambd = 100)
虽然图形十分曲折,但总体趋势是在下降且损失更低了。
6. LASSO 回归
和岭回归类似,但正则项使用的是 L1 范数。但绝对值就意味着不可导,不好优化。
$loss = l(w, b) + λ||W||,\quad\quad ||W|| = \sum |W|$
1
2
3
4
5
6
7
8
| from sklearn.linear_model import Lasso
def LassoRegression(degree,alpha):
pipeline = Pipeline([
("poly",PolynomialFeatures(degree = degree)),
("std_scaler",StandardScaler()),
("lasso_reg",Lasso(alpha=alpha))
])
return pipeline
|
alpha = 0
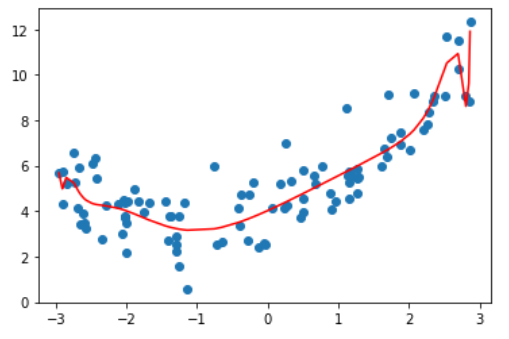
alpha = 0.1
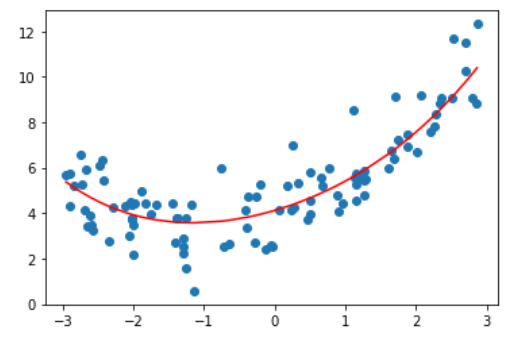
alpha = 1
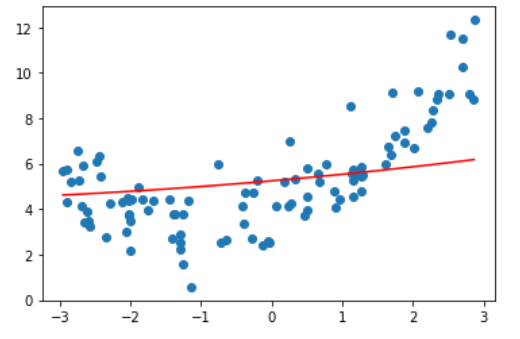
alpha = 10
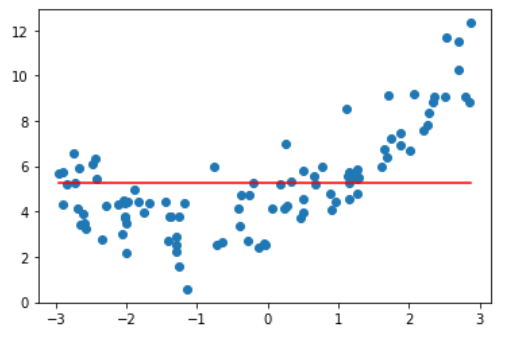
通过对比,可以发现一个比较有意思的事情。Ridge 回归在增大 alpha 时,曲线还是弯曲的,但没那么陡峭,因为权重都比较小。而 LASSO 回归在增大 alpha 时,并没有那么多弯曲的地方,因此它的权重大部分都是0。
至于为什么会这样呢?这也和他们正则化项的式子有关。
7. Ridge 和 LASSO 区别
Ridge 回归 的梯度是会随着离极值点越近而渐渐变小的,因此所有的参数是同步在更新,从图像上来看就是沿着梯度慢慢想极值点靠拢,因此不会有很多权重被设为0。
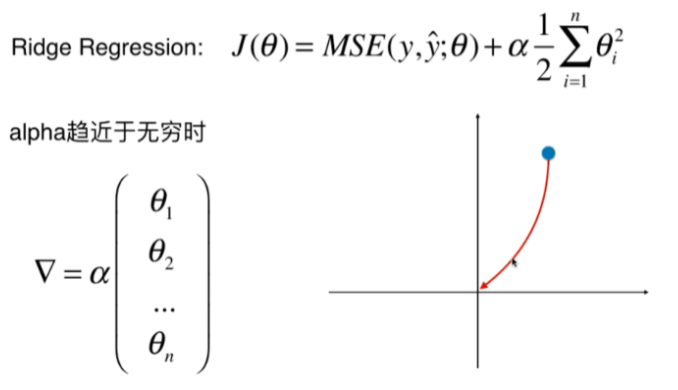
LASSO 回归 的梯度是一个定值,只能由 η 来控制大小,这样就会造成部分权重会早早停在零点,这可以起到一定的特征筛选的作用,虽然也有可能将有用的特征也筛选掉。

8. 弹性网络
顾名思义,是个弹性(折中)的网络,它结合岭回归和 LASSO 回归的思想。
$loss = l(w, b) + γλ||W|| + \frac{(1-γ)}{2}λ||W||^2,\quad\quad γ∈[0,1]$
γ 代表一种比率,取值为 0% ~ 100%,当γ = 0时,该弹性网络为岭回归;当γ = 1时,该弹性网络为 LASSO 回归。
二、丢弃法
1. 什么是丢弃法?
丢弃法,又称 DropOut,具体做法是在每一层输出后,随机将一定量的输出置为0。那么这么做的目的是为什么呢?
一个好的模型需要对输入数据的扰动鲁棒。
- 使用有噪音的数据等价于正则化。
- 丢弃法则是在层之间加入噪音,同时也降低了模型的容量。

诶,那么这时有人要问了,你这随机置为0,对x的期望都变掉了。为了防止这样的情况,我们不单单是对数据置0,对另一部分的数据也要改动,保证期望不变。
注:p 是一个概率值,将神经元置为0的比率,$p∈[0,1]$。
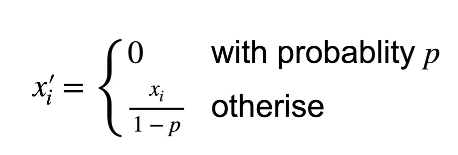
$$
Ex_i’ = p * X_i * 0 + (1-p) \frac{x_i}{1-p} = x_i
$$
左边没有 Dropout,右边有 Dropout。
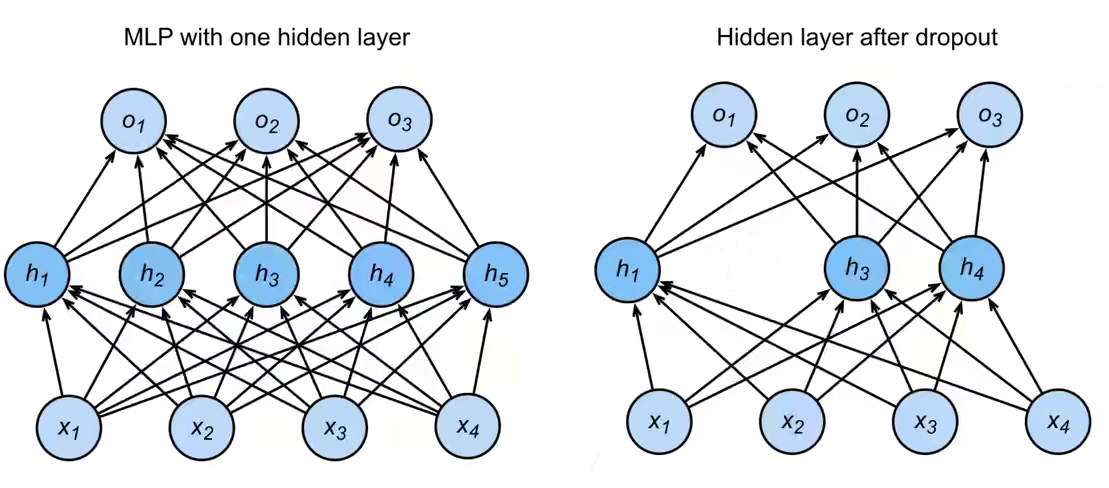
2.总结
- 丢弃法将一些输出项随机置0来控制模型复杂度。
- 常作用在多层感知机的隐藏层输出上。
- 丢弃概率是控制模型复杂度的超参数。
3. Tensorflow 实现
dropout层
1
2
3
4
5
6
7
8
9
10
11
| def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
if dropout == 1:
return tf.zeros_like(X)
if dropout == 0:
return X
mask = tf.random.uniform(X.shape, minval = 0, maxval = 1) < (1 - dropout)
return tf.cast(mask, dtype=tf.float32) * X / (1.0 - dropout)
|
测试 dropout
1
2
3
4
5
6
|
X = tf.reshape(tf.range(16, dtype=tf.float32), [2,8])
print(X)
print(dropout_layer(X, 0))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1))
|
模型定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| num_outputs = 10
num_hidden1 = 256
num_hidden2 = 256
dropout1 = 0.5
dropout2 = 0.5
class Net(tf.keras.Model):
def __init__(self, num_outputs, num_hidden1, num_hidden2):
super().__init__()
self.input_layer = keras.layers.Flatten()
self.hidden1 = keras.layers.Dense(num_hidden1, activation = "relu")
self.hidden2 = keras.layers.Dense(num_hidden2, activation = "relu")
self.output_layer = keras.layers.Dense(num_outputs, activation = "softmax")
def call(self, inputs, training=None):
X = self.input_layer(inputs)
X = self.hidden1(X)
if training:
X = dropout_layer(X, dropout1)
X = self.hidden2(X)
if training:
X = dropout_layer(X, dropout2)
X = self.output_layer(X)
return X
net = Net(num_outputs, num_hidden1, num_hidden2)
|
训练
这里说明一下损失函数的使用情况,我之前也一直没有注意过。
- SparseCategoricalCrossentropy 会给 label 做一个 one-hot 编码。
- CategoricalCrossentropy 不会给 label做 one-hot 编码。
- from_logits = True 用于最后输出层没有经过 softmax 的情况,会给结果补做一个 softmax。
1
2
3
4
5
6
7
8
| epochs = 10
lr = 0.5
batch_size = 256
loss = keras.losses.SparseCategoricalCrossentropy()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = keras.optimizers.SGD(learning_rate = lr)
d2l.train_ch3(net, train_iter, test_iter, loss, epochs, trainer)
|