紫梦沁香
0%

过拟合和欠拟合

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 4.6k 阅读时长 ≈ 8 分钟

引入

继之前的多项式回归，如果 degree 设置过大或者过小会出现什么样的问题呢？

在此之前，先来说明一下 归一化 的必要性。多项式回归采用了特征组合的方式，当 degree 为100时，最高次就是100次，而最低次只是常数级，各个维度数值之间的跨度非常大，这就导致 eta 必须设置得非常小，否则稍大一点，就会无法拟合，变成 nan 。

当 degree 为10时， eta就必须设置成$10^{-19}$，很不利于我们训练模型，所以在数据与距离阶段除了要多项式化还得归一化！

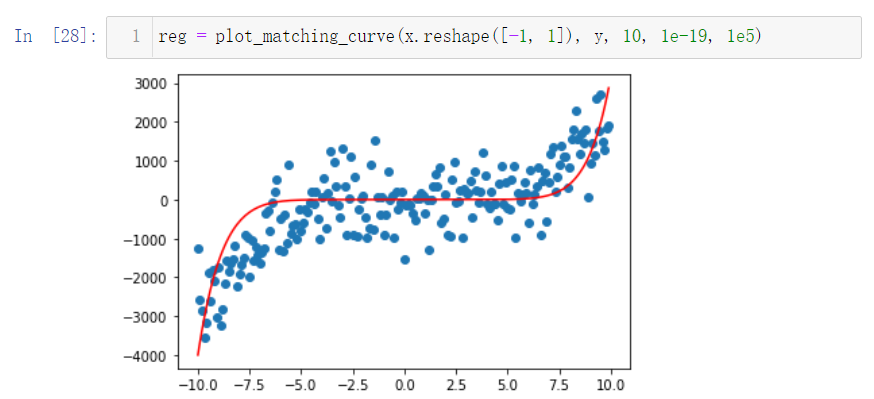
根据上述要求，改进了一下多项式回归的类。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class PolynomialRegression:
    
    def __init__(self, degree):
        self.degree = degree
        
    def fit(self, X, y, eta = 0.01, n_iters = 1e4, epsilon = 1e-6):
        self.X = self._getPolynomialFeatures(X, 0, np.ones([len(X), 1]), self.degree)
        self.X = self.standardization(self.X)
        
        initial_theta = np.zeros([self.X.shape[1]])
        theta = self._gradient_descent(self.X, y, initial_theta, eta, n_iters, epsilon)
        self.theta = theta
        self.coefficient = theta[1:]
        self.intercept = theta[0]
    
    # 归一化
    # 第一列全为1方差为0要单独处理，改成第一列全为0
    def standardization(self, X):
        return np.hstack([np.zeros([len(X), 1]), (X[:, 1:] - np.mean(X[:, 1:], axis = 0)) / np.std(X[:, 1:], axis = 0)])
    
    # 多项式化
    def _getPolynomialFeatures(self, X, start, col_val, degree):
        def dfs(X, result, start, col_val, degree):
            result.append(col_val)
            if(degree == 0):
                return

            for i in range(start, X.shape[1]):
                dfs(X, result, start, col_val * X[:, i].reshape([-1, 1]), degree - 1)
        
        result = []
        dfs(X, result, 0, np.ones([len(X), 1]), degree)
        return np.squeeze(np.array(result), -1).T
    
    # 预测也要多项式化和归一化
    def predict(self, X):
        X_b = self._getPolynomialFeatures(X, 0, np.ones([len(X), 1]), self.degree)
        X_b = self.standardization(X_b)
        y_pred = X_b.dot(self.theta)
        return y_pred
    
    # MSE
    def score(self, X, y):
        y_pred = self.predict(X)
        return np.mean((y - y_pred) ** 2)
        
    def _gradient_descent(self, X_b, y, theta, eta, n_iters, epsilon):
        
        def J(X_b, y, theta):
            return np.mean((X_b.dot(theta) - y) ** 2);

        def DJ(X_b, y, theta):
            return X_b.T.dot((X_b.dot(theta) - y)) * 2 / len(y);
        
        i_iter = 0
    
        while i_iter < n_iters:
            gradient = DJ(X_b, y, theta)
            last_theta = theta
            theta = theta - eta * gradient
            if np.abs(J(X_b, y, theta) - J(X_b, y, last_theta)) < epsilon:
                break
            i_iter += 1

        return theta

当然直接使用 sklearn 中的 Pipeline 可以更加简便的实现这一切。

Pipeline 具体运作机制就是逐行运行，上一行的输出就是下一行的输入，因此我们先进行多项式化，再归一化，最后放入线性回归中训练模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(X,y,degree):
    pipeline = Pipeline([
        ("poly",PolynomialFeatures(degree = degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",LinearRegression())
    ])
    pipeline.fit(X,y)
    return pipeline.predict(X)

数据拟合

先写一个绘制拟合曲线的函数便于我们观测结果。

1
2
3
4
5
6
7
8
9
def plot_matching_curve(X, y, degree, eta = 1e-6, n_iters = 1e5):
    poly_reg = PolynomialRegression(degree)
    poly_reg.fit(X, y, eta, n_iters)
    theta = poly_reg.theta
    pred_y = poly_reg.X.dot(theta)
    plt.scatter(X[:, 0], y)
    plt.plot(X[:, 0], pred_y, color = "r")
    plt.show()
    return poly_reg

当 degree 为0时，也就是最高次为0次，拟合曲线成一条直线，这就是欠拟合。

毕竟函数只有一个常数嘛，合理。

1
plot_matching_curve(x.reshape([-1, 1]), y, 0)

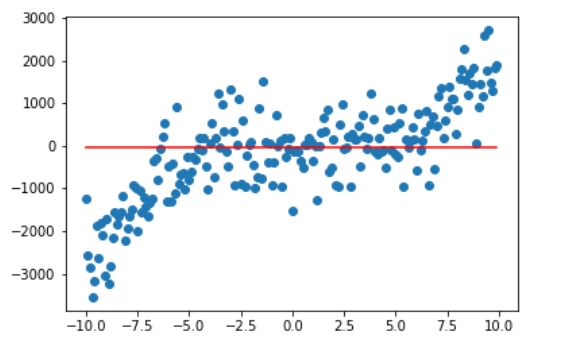
再来看看 degree 分别为1，2的情况，是不是越来越接近我们的拟合曲线了。

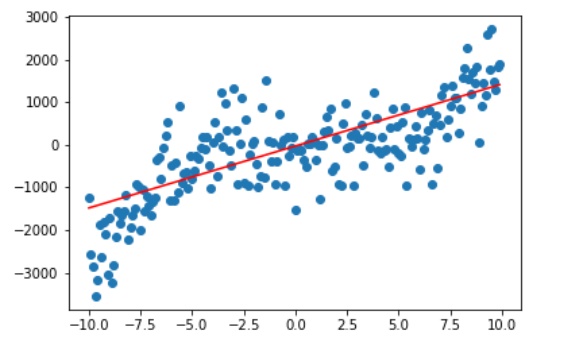
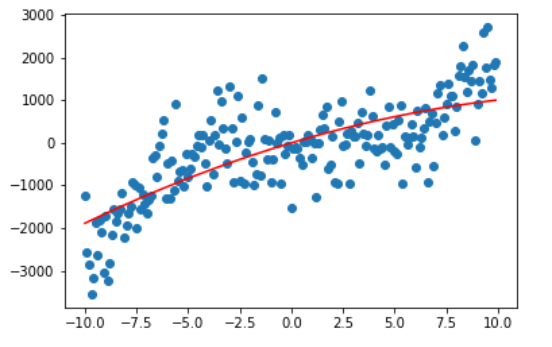
当 degree 为3时，曲线终于拟合了我们的数据。

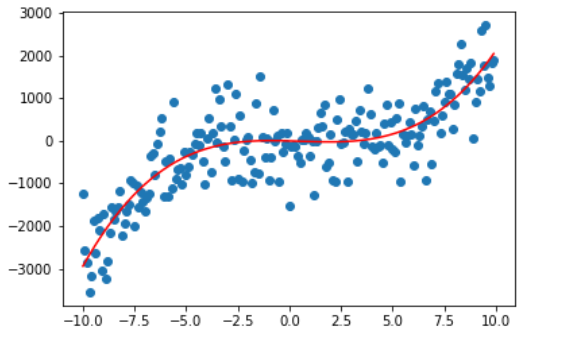
那我们再看看 degree 为10，50，100，200的情况。

很容易可以观察出，曲线变得越来越复杂，也越来越能拟合我们的训练数据，这是因为随着 degree 的增大，参数数量的增长使得我们的模型可以将训练的数据给记住，但这真的是我们想要的吗？

不，我们想要的是泛化能力，是在测试数据乃至之后模型上线后的真实数据上也能有非常好的预测能力。

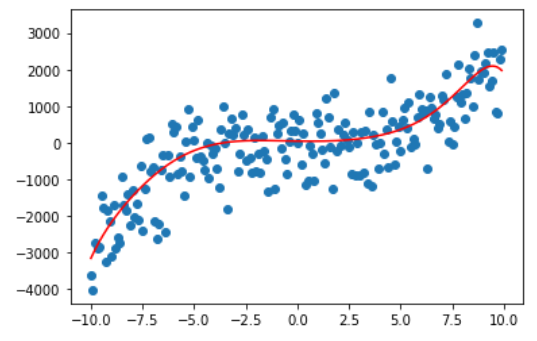
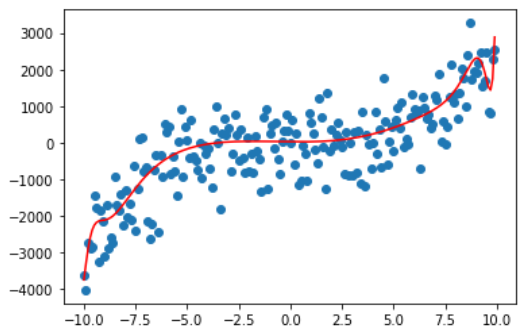
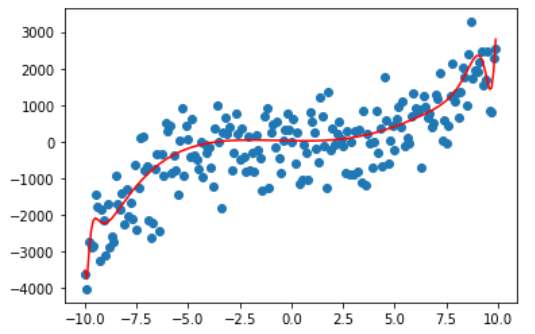
之前也说过了，多项式化是阶乘式地增长，一旦 degree 过大，直接就会导致栈溢出。


学习曲线

通过观察学习曲线，也可以帮助我们判断出模型是否有过拟合或欠拟合的情况。它是绘制模型在训练集和测试集上的性能函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression

def get_poly_reg(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree = degree)),
        ("std", StandardScaler()),
        ("reg", LinearRegression())
    ])

def plot_learning_curve(X, y, degree):
    train_mse = []
    test_mse = []
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    poly_reg = get_poly_reg(degree)
    
    for i in range(2, len(X) + 1):
        poly_reg.fit(X_train[:i], y_train[:i])
        train_pred = poly_reg.predict(X_train[:i])
        test_pred = poly_reg.predict(X_test)
        train_mse.append(np.mean(np.square(train_pred - y_train[:i])))
        test_mse.append(np.mean(np.square(test_pred - y_test)))
        
    plt.plot(np.arange(2, len(X)+1), train_mse, label="train")
    plt.plot(np.arange(2, len(X)+1), test_mse, label="test")
    plt.legend()
    plt.axis([0,100,0,5])
    plt.show()

这次我们把目标函数换成二次函数。

1
2
X = np.random.uniform(-3,3,size=100).reshape(-1,1)
y = 0.5 * X**2 + X + 4 + np.random.normal(0,1,size = 100).reshape(-1,1)

degree = 1

随着样本数量的增加 test 的误差在减小，train 的误差在增加，而当样本到了一定程度后，两者也没有保持在一个较小的程度上。这时说明模型欠拟合。

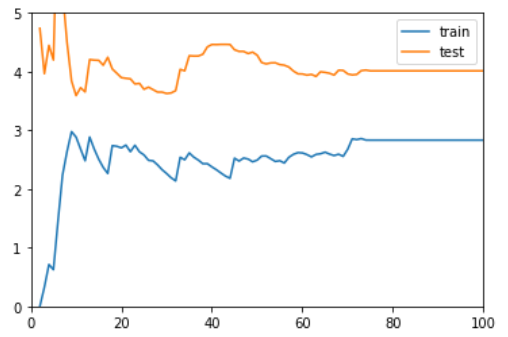
degree = 2

随着样本数量的增加 test 的误差在减小，train 的误差在增加，而当样本到了一定程度后，两者基本持平，保持在一个较小的程度上。这时模型已经拟合。

degree = 10

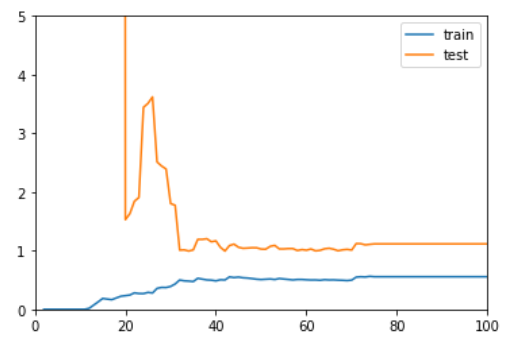
随着样本的增加 test 的误差在减小，train 的误差在增加，但当样本到了一定程度后，在 train 上的误差要比在 test 上的误差小得多，这时就要注意是不是过拟合了。

degree = 100

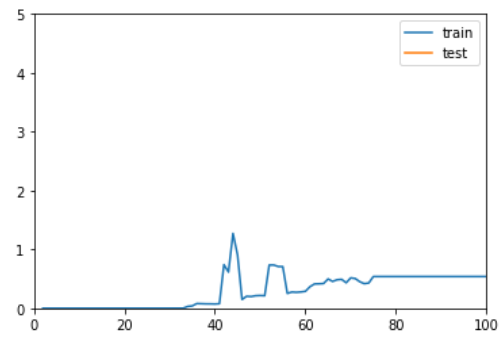
此时 test 上的误差已经飙到天上去了，妥妥的过拟合。

总结

在训练数据集上表现良好，却在测试数据集上表现差劲的就是过拟合，这时候要降低参数数量。

而在训练数据集上表现就不尽人意的有可能是欠拟合（也有可能是模型压根不对等问题），这时候可以试试增大模型，增加参数数量。