紫梦沁香
0%

数据归一化

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 3.5k 阅读时长 ≈ 6 分钟

算法思想

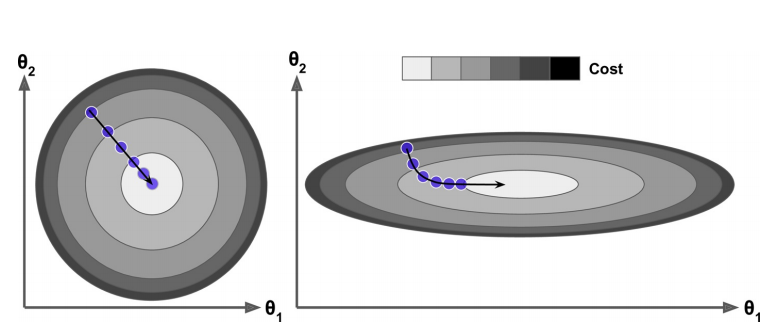
观察下图，可以发现每个特征之间的量纲不同，没有办法放在一起比较，学习出来的模型==可解释性比较差==（不会影响预测结果）。而且对于KNN算法来说，样本之间的距离极大部分会由发现时间（天）来引导，肿瘤大小（厘米）几乎可以忽略不计。

为此我们就需要采用归一化，把有量纲的表达式改成无量纲的表达式，将数据的所有特征都映射到一个统一的尺度下。（对于其它算法如线性回归则不会影响分类或预测结果）

而且归一化后可以加速训练，左侧因为进行了归一化，因此等高线几乎是正圆，等高线上的法线指向圆心，因此能快速收敛到最小值，而右图没有进行归一化则需进行多次迭代。

没有进行归一化，学习率也得按照特征取值范围最小的那个维度来取，不然很容易出现nan。

注：由于进行了归一化，我们的模型都是按照归一化的数据进行训练的，因此测试数据也要进行归一化，否则没有意义了。

（1） 均值方差归一化（standardization）
$$
X_{scale} = \frac{X - X_{mean}}{X_{std}}
$$
经过该标准化处理的数据，均值为0，方差为1，符合正态分布。

适用于数据分布没有明显的边界，有可能存在极端的数据值。

正好学了概率论，就来简单推导下吧。
$$
设经过均值方差归一化后X^的数学期望和方差分别为E^X, D^X \qquad (X^ = \frac{X - EX}{\sqrt{DX}})
\
E^X = E(\frac{X - EX}{\sqrt{DX}}) = \frac{1}{\sqrt{DX}} * (EX - EX) = 0
\
D^X = D(\frac{X - EX}{\sqrt{DX}}) = \frac{1}{DX} * D(X - EX) = \frac{1}{DX} * DX = 1
$$
（2）最值归一化（Normalization）
$$
X_{scale} = \frac{X - X_{min}}{X_{max} - X_{min}}
$$
经过该标准化处理的数据，数据分布在(0, 1)。

适用于分布有明显边界的情况，受 outliner影响较大。

例如像素范围（0 ~ 255），学生成绩（0 ~ 100）。


实例

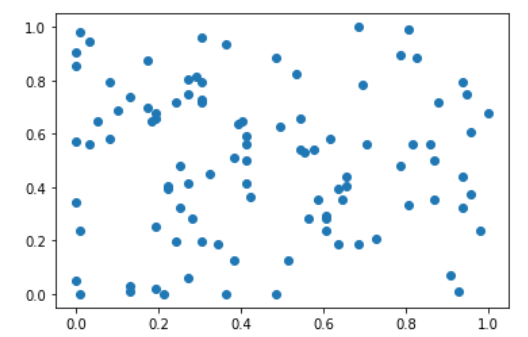
（1） 最值归一化

1
2
3
4
5
6
7
8
9
class MinMaxScaler:
    
    def fit(self, X):
        self.X = X
        self.max = np.max(X, axis = 0)
        self.min = np.min(X, axis = 0)
        
    def transform(self, X):
        return (X - self.min) / (self.max - self.min)

原始数据均值为46.995，标准差为27.97007284581147。

1
2
3
4
5
6
X = np.random.randint(0, 100, (100, 2))
print(np.mean(X))			# 46.995
print(np.std(X))			# 27.97007284581147

plt.scatter(X[:, 0], X[:, 1])
plt.show()

经过最值归一化后，均值为0.4721085858585859，标准差为0.2863025514861211。

所有值都被映射到（0， 1）之间

1
2
3
4
5
6
7
8
9
minMaxScaler = MinMaxScaler()
minMaxScaler.fit(X)
X1 = minMaxScaler.transform(X)

print(np.mean(X1))			# 0.4721085858585859
print(np.std(X1))			# 0.2863025514861211

plt.scatter(X1[:, 0], X1[:, 1])
plt.show()

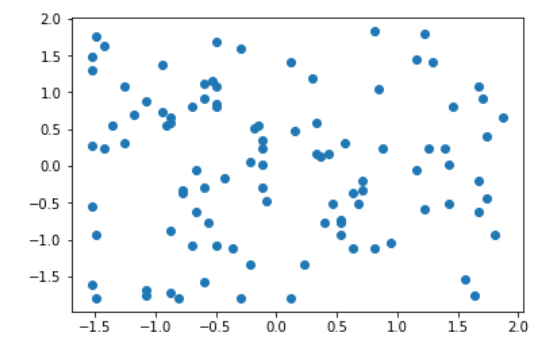
（2） 均值方差归一化

1
2
3
4
5
6
7
8
9
class StandardScaler:
    
    def fit(self, X):
        self.X = X
        self.mean = np.mean(X, axis = 0)
        self.std = np.std(X, axis = 0)
        
    def transform(self, X):
        return (X - self.mean) / self.std

经过均值方差归一化后，均值几乎为0，标准差也几乎为1，但数据范围不一定在（0， 1）中。

1
2
3
4
5
6
7
8
9
standardScaler = StandardScaler()
standardScaler.fit(X)
X1 = standardScaler.transform(X)

print(np.mean(X1))				# -2.7755575615628914e-17
print(np.std(X1))				# 0.9999999999999998

plt.scatter(X1[:, 0], X1[:, 1])
plt.show()

测试

先介绍一下 train test split，正如它的字面意思。将一份数据集分成训练数据集和测试数据集，这样在使用 score 函数时，使用的都是训练时没有见过的数据集，得出来的准确率也就更可靠。

首先数据集需要打乱，因为有些数据集是根据类别来分类的，例如前 k 个都是类别1，后 k 个都是类别2，这样 train 和test中的类别分布差距很大，会导致泛化效果不好。

np.random.seed(seed) 使用同一个种子为了能更好的比较使用归一化和不使用归一化的区别。

1
2
3
4
5
def train_test_split(X, y, split_rate, seed):
    np.random.seed(seed)
    length = int(len(X) * split_rate)
    p = np.random.permutation(len(X))
    return X[p[length:]], X[p[:length]], y[p[length:]], y[p[:length]]

（1） 不使用归一化进行学习

1
2
3
4
5
6
7
8
9
10
boston=datasets.load_boston()
X=boston.data			# (506, 13)
y=boston.target			# (506, )

split_rate = 0.2
X_train, X_test, y_train, y_test = train_test_split(X, y, split_rate)

lr = LinearRegression()
lr.fit(X_train, y_train, eta = 1e-6, n_iters = 1e6)
lr.score(X_test, y_test)

eta = 1e-6

score = 31.348463775149956

（2） 使用最值归一化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
boston=datasets.load_boston()
X=boston.data
y=boston.target

minMaxScaler = MinMaxScaler()
minMaxScaler.fit(X)
X = minMaxScaler.transform(X)

split_rate = 0.2
X_train, X_test, y_train, y_test = train_test_split(X, y, split_rate)

lr = LinearRegression()
lr.fit(X_train, y_train, eta = 1e-2, n_iters = 1e6)
lr.score(X_test, y_test)

eta = 1e-2

score = 25.209485526542817

（3） 使用均值方差归一化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
boston=datasets.load_boston()
X=boston.data
y=boston.target

standardScaler = StandardScaler()
standardScaler.fit(X)
X = standardScaler.transform(X)

split_rate = 0.2
X_train, X_test, y_train, y_test = train_test_split(X, y, split_rate)

lr = LinearRegression()
lr.fit(X_train, y_train, eta = 1e-2, n_iters = 1e6)
lr.score(X_test, y_test)

eta = 1e-2

score = 18.92473923096906

经过对比，使用同样的训练次数，经过了归一化的预测率明显比没有经过归一化的预测率更高，而且eta取1e-2就行，不用多次尝试。