紫梦沁香
0%

KNN算法

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 6.4k 阅读时长 ≈ 12 分钟

1、KNN算法

KNN算法需要先给定一组带有标签的数据，需要预测的数据只需和现有的样本测出 “距离”，选出最近的 K 个，综合这 K 个样本中的标签做出预测即可。

当 K <= 0 时无意义，当 K = 1 时即将距离待预测数据最近的样本标签值作为预测结果，而当 K = n（n为样本数量）时，就失去了投票的意义，永远都只会预测一个值，就是样本中标签最多的那个值！

如果是分类问题就选择多数的那个样本类别，是回归问题就取平均值即可（也可根据距离进行加权，距离越近权重越大）。

因此在分类问题中，K的选择一般都是==奇数==，不然出现平票就很尴尬了。

KNN 和其他大多数机器学习算法有所不同，就在于它没有训练模型的过程！！！KNN 模型只需要将训练集中的样本全部保存下来就完成了，而将大部分时间都放在了预测数据上！！

==注：KNN 全称 K-Nearest Neighbor，也叫作K近邻算法。==


2、分类问题

2.1、投票流程

先随机生成 100 个具有 两个 特征的样本作为数据集，人为地将 左下角（x < 5 && y < 5） 的数据归为 ==类别1==（红点），其它的数据归为 ==类别二==（蓝点）。

1
2
3
4
5
6
7
8
9
10
11
# 为了实验的可重复性，这里使用了随机种子（撒旦）
np.random.seed(666)
x1 = np.random.random(100) * 10
x2 = np.random.random(100) * 10

# y为类别一，~y为类别二
y = (x1 < 5) & (x2 < 5)

plt.scatter(x1[y], x2[y], color = "red")
plt.scatter(x1[~y], x2[~y], color = "blue")
plt.show()

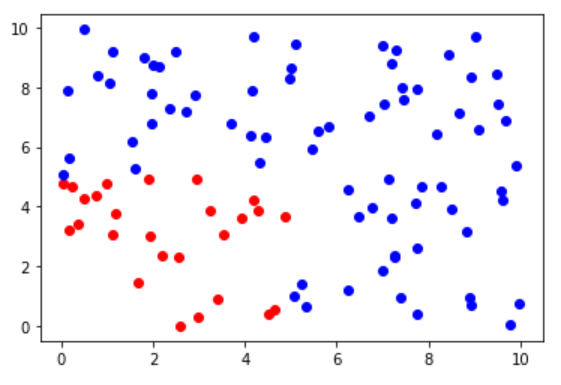
image

再随机生成一个 z 点（绿点）作为待预测数据，观察 z 点位于整个数据集中的分布，很容易可以判断出其应该属于 ==类别二==（蓝点）。

1
2
3
4
5
6
7
8
# z点
z_x1 = np.random.random() * 10
z_x2 = np.random.random() * 10

plt.scatter(x1[y], x2[y], color = "red")
plt.scatter(x1[~y], x2[~y], color = "blue")
plt.scatter(z_x1, z_x2, color = "green")
plt.show()

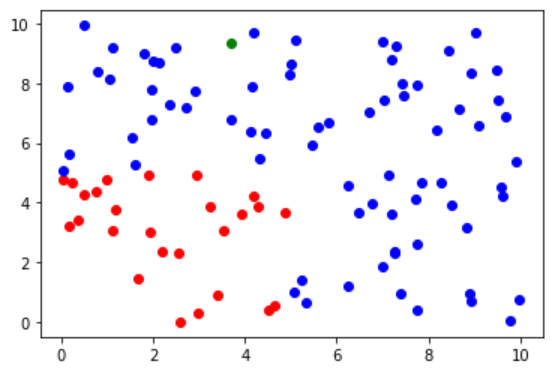
image

根据待预测样本周围 K 个数据（这里使用的是欧氏距离 $d = \sqrt{(x - x_1)^2 +(x-x_2)^2}$）的投票情况预测分类结果，代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 求出与其它所有样本的欧拉距离（或者用曼哈顿距离或闵可夫斯基距离也可以）
distance = np.sqrt(np.square(x1 - z_x1) + np.square(x2 - z_x2))

# 根据距离排序，这里只需要排序后样本的下标
distance_nearest = np.argsort(distance)

# 这里K取6，使用Counter库进行统计，y[distance_nearest[:6]]就是距离前6的样本
counter = Counter(y[distance_nearest[:6]])

# label即距离前6的样本中投票最多样本
label = counter.most_common(1)[0][0]

# label=0对应蓝色，label=1对应红色
color = ""
if label == 0:
    color = "blue"
else:
    color = "red"

# 绘制图像
plt.scatter(x1[y], x2[y], color = "red")
plt.scatter(x1[~y], x2[~y], color = "blue")
plt.scatter(z_x1, z_x2, color = color)
plt.show()

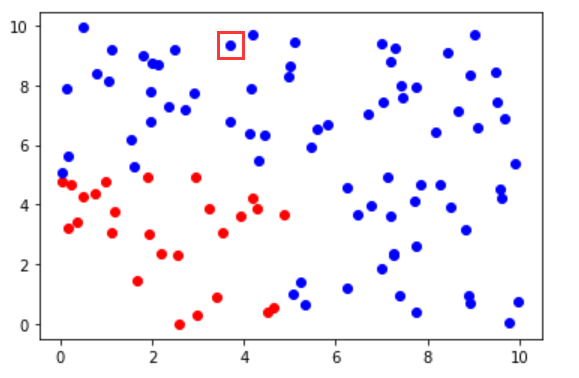
可以看到原先绿色的样本，现在的预测结果为蓝色（红色框框出来的那个点），预测正确。

image

2.2、归一化

先来看一下面的这个例子，通过性别身高来预测年龄（暂且不用关注只用这两个特征是否真的能准确预测出年龄），而身高根据单位的不同，值也有所不同。当身高单位取厘米时，距离大小几乎由身高所主导；而身高单位取千米时（虽然现实生活中不会这么取），距离大小又会被性别所主导。这样就导致训练的模型==可解释性比较差==，无法正确反映各个特征对结果的重要程度。

性别（0女，1男） 身高 年龄
样本1 1 175cm = 1.75m = 0.00175km ？
样本2 0 165cm = 1.65m = 0.00165km ？

由此就引入了归一化，可以将 有量纲 的特征转变为 无量纲 的特征（对于其他机器学习算法归一化还可以加速收敛），==当然不加归一化不会影响预测结果==。

下面介绍两种归一化的方法。

（1） 均值方差归一化（standardization）
$$
X_{scale} = \frac{X - X_{mean}}{X_{std}}
$$
经过该标准化处理的数据，均值为0，方差为1，符合正态分布。

适用于数据分布没有明显的边界，有可能存在极端的数据值。

推导如下：
$$
设经过均值方差归一化后X^的数学期望和方差分别为E^X, D^X \qquad (X^ = \frac{X - EX}{\sqrt{DX}})
\
E^X = E(\frac{X - EX}{\sqrt{DX}}) = \frac{1}{\sqrt{DX}} * (EX - EX) = 0
\
D^X = D(\frac{X - EX}{\sqrt{DX}}) = \frac{1}{DX} * D(X - EX) = \frac{1}{DX} * DX = 1
$$

（2）最值归一化（Normalization）
$$
X_{scale} = \frac{X - X_{min}}{X_{max} - X_{min}}
$$
经过该标准化处理的数据，数据分布在(0, 1)。

适用于分布有明显边界的情况，受 outliner影响较大。

例如像素范围（0 ~ 255），学生成绩（0 ~ 100）。


2.2、代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class KNNClassifier:
    
    # 传入超参数K
    def __init__(self, neighbour):
        self.neighbour = neighbour
        
    # 归一化
    def standardization(self, X):
        return (X - self.mean) / self.std
        
    # 如上文所述，没有训练过程，只需要保存数据集即可
    def fit(self, X, y):
        self.mean = np.mean(X, axis = 0)
        self.std = np.std(X, axis = 0)
        self.data = self.standardization(X)
        self.label = y
        
    # 预测
    def _predict(self, X):
        distance = [np.sqrt(np.sum(np.square(X_data - X))) for X_data in self.data]

        # 返回距离前K个样本的投票结果
        distance_sorted_idx = np.argsort(distance)
        distance_sorted_idx_top_k = distance_sorted_idx[:self.neighbour]
        counter = Counter(self.label[distance_sorted_idx_top_k])
        return counter.most_common(1)[0][0]
        
    def predict(self, X_test):
        X_test = self.standardization(X_test)
        res = [self._predict(x) for x in X_test]
        return np.array(res)
    
    # 评估测试结果
    def score(self, X, y):
        return np.sum(self.predict(X) == y) / len(X)

2.3、代码测试

测试我选用了稍微真实一点的数据集，sklearn 中的鸢尾花数据集。

1
2
3
4
5
6
7
from sklearn.datasets import load_iris

iris = load_iris()
X = iris["data"]
y = iris["target"]
print(X.shape)	# (150, 4)
print(y.shape)	# (150, )

鸢尾花分布如下，为了便于展示，这里只显示了两个特征。

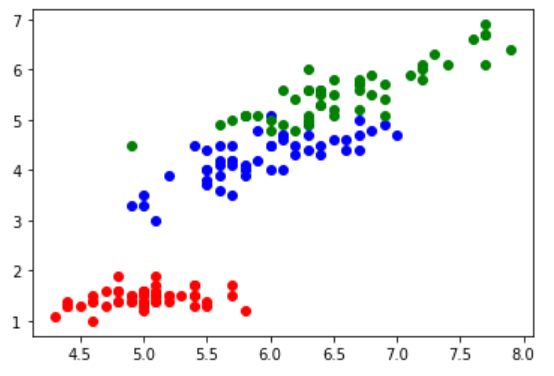
image

先将整个数据集分割成训练集和测试集（也可以再多分一份，做成验证集做交叉验证，这里数量量太少没太大意义）。

1
2
3
4
5
6
7
def train_test_split(X, y, rate = 0.8):
    gap = len(X) * rate
    # 打乱以防原有数据有规律
    shuffle_indexes = np.random.permutation(len(X))
    train_idx = shuffle_indexes[:gap]
    test_idx = shuffle_indexes[gap:]
    return X[train_idx], y[train_idx], X[test_idx], y[test_idx]

然后将我们的模型在测试集上进行预测，96.7% 还是很不错的预测率。

1
2
3
4
5
X_train, y_train, X_test, y_test = train_test_split(X, y)
knn_clf = KNNClassifier(4)
knn_clf.fit(X_train, y_train)
print(knn_clf.predict(X_test))	# [0 2 2 1 0 1 0 0 0 0 0 2 1 2 0 0 2 2 1 0 2 0 2 1 2 1 2 2 2 1]
print(knn_clf.score(X_test, y_test))	# 0.9666666666666667

2.4、网格化搜索

不过超参数 K 到底应该如何取值呢？一般我们可以通过 经验法则 或者是 网格化搜索 来寻找最合适的超参数（其实就是暴力枚举各个超参数下的预测率，取最好的那个）。但在绝大部分情况下，超参数的取值都是无穷无尽的，需要人为定义遍历范围。

1
2
3
4
5
6
7
8
9
10
11
best_K = -1
best_score = -1
for i in range(1, 10):
    knn_clf = KNNClassifier(i)
    knn_clf.fit(X_train, y_train)
    if knn_clf.score(X_test, y_test) > best_score:
        best_score = knn_clf.score(X_test, y_test)
        best_K = i
        
print("best_K =", str(best_K))	# best_K = 1
print("best_score =", str(best_score))	# best_score = 0.9666666666666667

3、回归问题

当然也可以使用 KNN 来解决回归问题，与分类问题类似，也是选取附近 K 个样本，然后取平均值就行了。如果讲究一点的话，还可以根据每个样本距离待预测数据的远近来设置权重，求加权平均。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class KNNRegression:
    
    # 传入超参数K
    def __init__(self, neighbour):
        self.neighbour = neighbour
        
    # 归一化
    def standardization(self, X):
        return (X - self.mean) / self.std
        
    # 如上文所述，没有训练过程，只需要保存数据集即可
    def fit(self, X, y):
        self.mean = np.mean(X, axis = 0)
        self.std = np.std(X, axis = 0)
        self.y_mean = np.mean(y)
        self.data = self.standardization(X)
        self.label = y
        
    # 预测
    def _predict(self, X):
        distance = [np.sqrt(np.sum(np.square(X_data - X))) for X_data in self.data]

        # 返回距离前K个样本的投票结果
        distance_sorted_idx = np.argsort(distance)
        distance_sorted_idx_top_k = distance_sorted_idx[:self.neighbour]
        return np.mean(self.label[distance_sorted_idx_top_k])
        
    def predict(self, X_test):
        X_test = self.standardization(X_test)
        res = [self._predict(x) for x in X_test]
        return np.array(res)
    
    # 回归问题用R^2预测分数会比较直观一点
    def score(self, X, y):
        return 1 - np.sum((y - self.predict(X)) ** 2) / np.sum((self.y_mean - self.predict(X)) ** 2)

这次使用 sklearn 中的波士顿房产数据集进行训练，步骤大体都和分类问题一致，下面只给出代码以及结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.datasets import load_boston
boston = load_boston()
X = boston["data"]
y = boston["target"]
print(X.shape)	# (506, 13)
print(y.shape)	# (506, )

best_K = -1
best_score = -1
for i in range(1, 10):
    knn_reg = KNNRegression(i)
    knn_reg.fit(X_train, y_train)
    if knn_reg.score(X_test, y_test) > best_score:
        best_score = knn_reg.score(X_test, y_test)
        best_K = i
        
print("best_K =", str(best_K))	# best_K = 1
print("best_score =", str(best_score))	# best_score = 0.9566003616636528

4、小结

通过上述两个小例子可以发现，每预测一个数据就需要和训练集中的所有样本求距离，而当我们的训练集十分庞大时，这个时间开销是不可估量的，而这还仅仅只是预测一个数据而已。因此可以用两个词来概括 KNN 算法——==简单但效率低==。