梯度下降法

算法思想

梯度下降法是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。（PS：梯度上升法解决最大化问题）

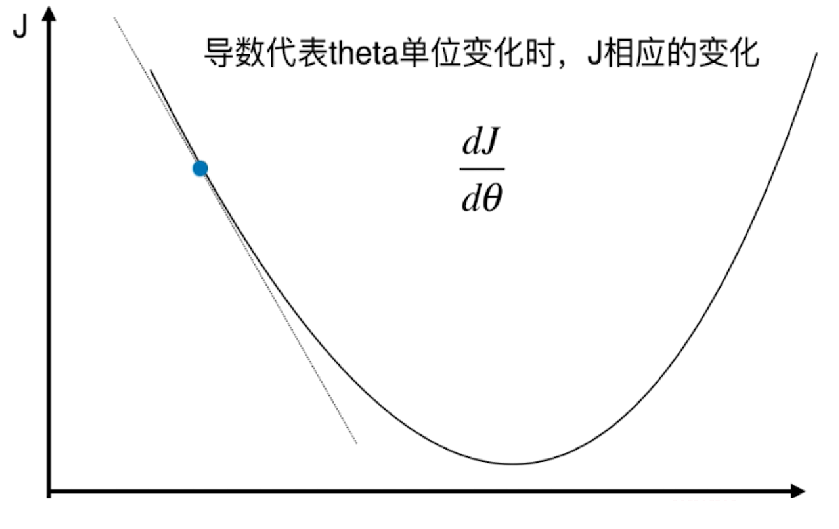
斜率为正，代表单调递增，说明极值点在左边；

斜率为负，代表单调递减，说明极值点在右边。

因此我们可以通过减去导数来找到最值点（假如极值点只有一个），因此被称为梯度下降法。

不过由于每个点上的导数是固定的，例如接近笔直的直线斜率就几乎是无穷大，如果我们直接减去导数，显然就不大合适。

所以就引申出了eta，也被称作学习率（learning rate）。现在我们只需减去eta * gradient就可以了，通过调整eta的大小来改变拟合的速度

eta过大可能导致无法拟合，eta过小则会拟合过慢，下面会有实例展示。

实例

这是eta适中的情况，只花了26步就找到了最小值。

start = -10.0
epsilon = 1e-5
eta = 0.4

# 26 steps
plot_gradient_tracks(start, epsilon, eta)

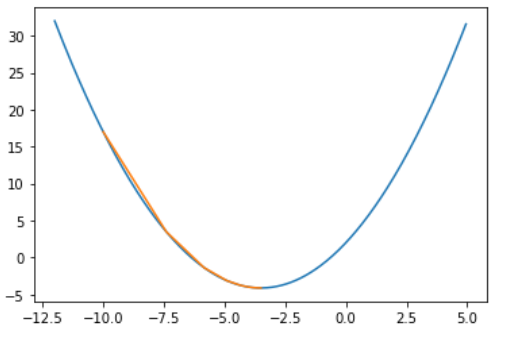
这里eta就偏小了，虽然也能找到最小值，但运行了875次，是上面的五十多倍。

start = -10.0
epsilon = 1e-5
eta = 0.01

# 875 steps
plot_gradient_tracks(start, epsilon, eta)

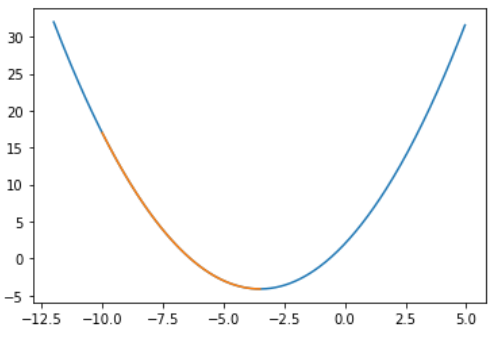
这里eta也算是适中的情况，只不过图像会比较特殊，左右反复横跳，因此我也拿出来当个样例。

start = -10.0
epsilon = 1e-5
eta = 1.5

# 21 steps
plot_gradient_tracks(start, epsilon, eta)

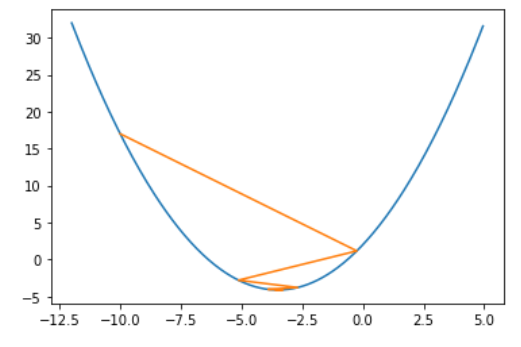
这是最差的情况，eta过大，导致y越来越大，已经无法取得最小值了。

start = -10.0
epsilon = 1e-5
eta = 2.5

plot_gradient_tracks(start, epsilon, eta, max_len = 4)

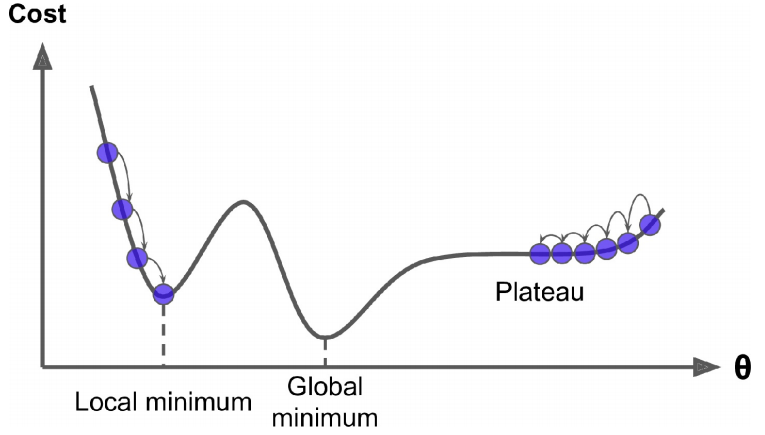
当然也会有存在多个极值点的情况，下图中如果选择左边作为起始点，基本就找不到全局最优解了，只能找到局部最优解。

不过幸好，一般使用MSE(Mean Square Error)作为成本函数，而MSE恰好是个凸函数，这就意味着连接曲线上任意两点的线段永远也不会跟曲线相交。也就是说不存在局部最小值，只有一个全局最小值。它同时也是一个连续函数，所以斜率不会产生陡峭的变化。

这两点保证的结论是：即便是乱走，梯度下降也可以趋近到全局最小值（只要等待时间足够长，学习率也不是太高）。

代码实现

import numpy as np
import matplotlib.pyplot as plt

# 目标函数
def J(x):
    return 0.5 * x ** 2 + 3.5 * x + 2

# 目标导函数
def DJ(x):
    return x + 3.5

# 绘制导数轨迹曲线
def plot_gradient_tracks(start, epsilon, eta, max_len = 1e4):
    a = start

    historys = []
    while(max_len > 0):
        last = J(a)
        historys.append([a, J(a)])
        a = a - eta * DJ(a)
        if np.abs(last - J(a)) < epsilon:
            break
        max_len -= 1

    historys = np.array(historys)
    plt.plot(x, y)
    plt.plot(historys[:, 0], historys[:, 1])
    plt.show()
    print(historys.shape[0])
    return historys[-1]

测试

start = -10.0
epsilon = 1e-5
eta = 1.5

plot_gradient_tracks(start, epsilon, eta)		# array([-3.5000062, -4.125])

将目标函数配方得，$\frac{1}{2}x^2 + \frac{7}{2}x + 2 = \frac{1}{2}[(x + \frac{7}{2})^2 + \frac{33}{4}]$

可以得出在$x = -\frac{7}{2}$处，取得最小值$y = \frac{33}{8}$

与测试结果基本一致。

注：计算结果不可能与理论值相等。